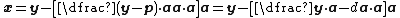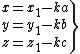- Converting general problem to distance-from-origin problem
- Restatement using linear algebra
- Why this is the closest point
- Closest point and distance for a hyperplane and arbitrary point
- See also
- References
In Euclidean space, the point on a plane 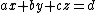 that is closest to the origin has the Cartesian coordinates
that is closest to the origin has the Cartesian coordinates  , where
, where
.{{Citation needed|date=January 2016}}
The distance between the origin and point  is
is 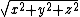 .
.
If what is desired is the distance from a point not at the origin to the nearest point on a plane, this can be found by a change of variables that moves the origin to coincide with the given point.
Converting general problem to distance-from-origin problem
Suppose we wish to find the nearest point on a plane to the point ( ), where the plane is given by
), where the plane is given by 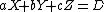 . We define
. We define 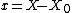 ,
, 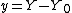 ,
, 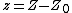 , and
, and 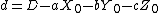 , to obtain
, to obtain 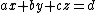 as the plane expressed in terms of the transformed variables. Now the problem has become one of finding the nearest point on this plane to the origin, and its distance from the origin. The point on the plane in terms of the original coordinates can be found from this point using the above relationships between
as the plane expressed in terms of the transformed variables. Now the problem has become one of finding the nearest point on this plane to the origin, and its distance from the origin. The point on the plane in terms of the original coordinates can be found from this point using the above relationships between  and
and 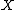 , between
, between  and
and  , and between
, and between  and
and  ; the distance in terms of the original coordinates is the same as the distance in terms of the revised coordinates.
; the distance in terms of the original coordinates is the same as the distance in terms of the revised coordinates.
Restatement using linear algebra
The formula for the closest point to the origin may be expressed more succinctly using notation from linear algebra. The expression 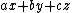 in the definition of a plane is a dot product
in the definition of a plane is a dot product 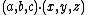 , and the expression
, and the expression 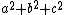 appearing in the solution is the squared norm
appearing in the solution is the squared norm 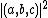 . Thus, if
. Thus, if 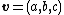 is a given vector, the plane may be described as the set of vectors
is a given vector, the plane may be described as the set of vectors  for which
for which 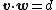 and the closest point on this plane is the vector
and the closest point on this plane is the vector
.[1][2]
The Euclidean distance from the origin to the plane is the norm of this point,
.
Why this is the closest point
In either the coordinate or vector formulations, one may verify that the given point lies on the given plane by plugging the point into the equation of the plane.
To see that it is the closest point to the origin on the plane, observe that  is a scalar multiple of the vector
is a scalar multiple of the vector  defining the plane, and is therefore orthogonal to the plane.
defining the plane, and is therefore orthogonal to the plane.
Thus, if  is any point on the plane other than
is any point on the plane other than  itself, then the line segments from the origin to
itself, then the line segments from the origin to  and from
and from  to
to  form a right triangle, and by the Pythagorean theorem the distance from the origin to
form a right triangle, and by the Pythagorean theorem the distance from the origin to  is
is
.
Since 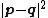 must be a positive number, this distance is greater than
must be a positive number, this distance is greater than 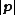 , the distance from the origin to
, the distance from the origin to  .[2]
.[2]
Alternatively, it is possible to rewrite the equation of the plane using dot products with  in place of the original dot product with
in place of the original dot product with  (because these two vectors are scalar multiples of each other) after which the fact that
(because these two vectors are scalar multiples of each other) after which the fact that  is the closest point becomes an immediate consequence of the Cauchy–Schwarz inequality.[1]
is the closest point becomes an immediate consequence of the Cauchy–Schwarz inequality.[1]
Closest point and distance for a hyperplane and arbitrary point
The vector equation for a hyperplane in  -dimensional Euclidean space
-dimensional Euclidean space  through a point
through a point  with normal vector
with normal vector 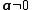 is
is 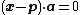 or
or  where
where 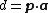 .[3]
.[3]
The corresponding Cartesian form is 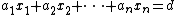 where
where 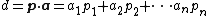 .[3]
.[3]
The closest point on this hyperplane to an arbitrary point  is
is
and the distance from  to the hyperplane is
to the hyperplane is
.[3]
Written in Cartesian form, the closest point is given by 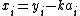 for
for  where
where
,
and the distance from  to the hyperplane is
to the hyperplane is
.
Thus in  the point on a plane
the point on a plane 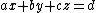 closest to an arbitrary point
closest to an arbitrary point 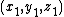 is
is  given by
given by
where
,
and the distance from the point to the plane is
.
See also
- Distance from a point to a line
- Hesse normal form
- Skew lines#Distance
References
2. ^1 {{citation|title=Linear Algebra: A Geometric Approach|first1=Ted|last1=Shifrin|first2=Malcolm|last2=Adams|edition=2nd|publisher=Macmillan|year=2010|isbn=9781429215213|page=32|url=https://books.google.com/books?id=QwHcZ7cegD4C&pg=PA32}}.
3. ^1 2 {{cite book|last1=Cheney|first1=Ward|last2=Kincaid|first2=David|title=Linear Algebra: Theory and Applications|date=2010|publisher=Jones & Bartlett Publishers|isbn=9781449613525|pages=450,451}}
- 986 CE
- 98.6 (disambiguation)
- 986 (year)
- (98713) 2000 XH43
- 987 AD
- 987 CE
- 98.7 Sea FM
- 987 (year)
- 98866 Giannabussolari
- 9887 Ashikaga
- 988 AD
- 988 Appella
- 988 CE
- 988 (year)
- 9898 Yoshiro
- 989 AD
- 989 CE
- 989 (year)
- 98 CE
- 98 (disambiguation)
- 98five Sonshine FM
- 98 KUPD
- 98 Piscium
- 98th (Argyllshire Highlanders) Regiment of Foot
- 98th Aviation Troop Command