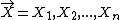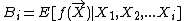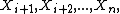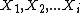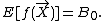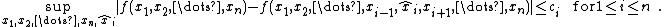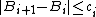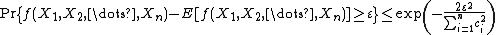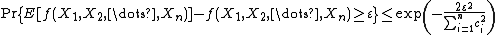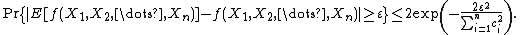1. Definition

2. Application

3. McDiarmid's inequality

4. See also

5. Notes

6. References

A Doob martingale (also known as a Levy martingale) is a mathematical construction of a stochastic process which approximates a given random variable and has the martingale property with respect to the given filtration. It may be thought of as the evolving sequence of best approximations to the random variable based on information accumulated up to a certain time.

When analyzing sums, random walks, or other additive functions of independent random variables, one can often apply the central limit theorem, law of large numbers, Chernoff's inequality, Chebyshev's inequality or similar tools. When analyzing similar objects where the differences are not independent, the main tools are martingales and Azuma's inequality.{{Clarify|reason=what has this para to do with Doob martingale in particular|date=May 2012}}

Definition

A Doob martingale (named after Joseph L. Doob)^[1]

is a generic construction that is always a martingale. Specifically, consider any set of random variables

taking values in a set for which we are interested in the function 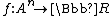and define:

where the above expectation is itself a random quantity since the expectation is only taken over

and

are treated as random variables. It is possible to show that is always a martingale regardless of the properties of .{{Citation needed|date=May 2012}}

The sequence 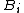is the Doob martingale for f.^[2]

Application

Thus if one can bound the differences

,

one can apply Azuma's inequality and show that with high probability 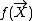is concentrated around its expected value

McDiarmid's inequality

One common way of bounding the differences and applying Azuma's inequality to a Doob martingale is called McDiarmid's inequality.^[3]

Suppose are independent and assume that

satisfies

(In other words, replacing the -th coordinate by some other value changes the value of

by at most .)

It follows that

and therefore Azuma's inequality yields the following McDiarmid inequalities for any :

and

and

See also

• Concentration inequality - a summary of McDiarmid's and several similar inequalities.

Notes

References

• {{cite journal |last=McDiarmid |first=Colin |year=1989 |title=On the Method of Bounded Differences |journal=Surveys in Combinatorics |volume=141 |issue= |pages=148–188 |url=http://www.stats.ox.ac.uk/people/academic_staff/colin_mcdiarmid/?a=4113 }}

• Tevita Mafileo
• Tevita Nabura
• Tevita Ngalu
• Tevita Pangai
• Tevita Pangai Jr
• Tevita Pangai Junior
• Tevita Satae
• Tevita Tatola
• Tevita Taufo'ou
• Tevita Taufoou
• Tevita Taufu’i
• Tevita Tawai
• Tevita Tu'ifua
• Tevita Tukimaka
• Tevita Va`enuku
• Tevita Vakatapu
• Tevita Vonolagi
• Tevita Wanono Tawai
• Tevita Waranaivalu
• Tevki
• Te'Von Coney
• Te'von Coney
• Tevorangh
• Te voy a ensenar a querer
• TEVp