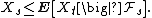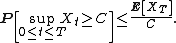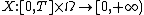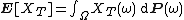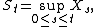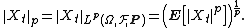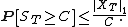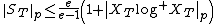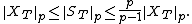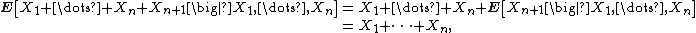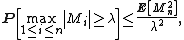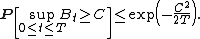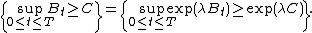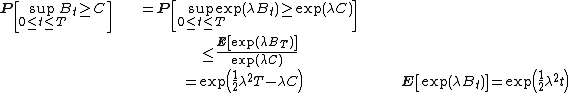“Doob's martingale inequality”的意思、由来-开放百科全书

词条

Doob's martingale inequality

释义

Statement of the inequality
Further inequalities
Related inequalities
Application: Brownian motion
References

In mathematics, Doob's martingale inequality is a result in the study of stochastic processes. It gives a bound on the probability that a stochastic process exceeds any given value over a given interval of time. As the name suggests, the result is usually given in the case that the process is a non-negative martingale, but the result is also valid for non-negative submartingales.

The inequality is due to the American mathematician Joseph L. Doob.

Statement of the inequality

Let X be a submartingale taking non-negative real values, either in discrete or continuous time. That is, for all times s and t with s < t,

(For a continuous-time submartingale, assume further that the process is càdlàg.) Then, for any constant C > 0,

In the above, as is conventional, P denotes the probability measure on the sample space Ω of the stochastic process

and E denotes the expected value with respect to the probability measure P, i.e. the integral

in the sense of Lebesgue integration. 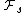denotes the σ-algebra generated by all the random variables X_i with i ≤ s; the collection of such σ-algebras forms a filtration of the probability space.

Further inequalities

There are further (sub)martingale inequalities also due to Doob. With the same assumptions on X as above, let

and for p ≥ 1 let

In this notation, Doob's inequality as stated above reads

The following inequalities also hold, : for p = 1,

and, for p > 1,

Related inequalities

Doob's inequality for discrete-time martingales implies Kolmogorov's inequality: if X₁, X₂, ... is a sequence of real-valued independent random variables, each with mean zero, it is clear that

so M_n = X₁ + ... + X_n is a martingale. Note that Jensen's inequality implies that |M_n| is a nonnegative submartingale if M_n is a martingale. Hence, taking p = 2 in Doob's martingale inequality,

which is precisely the statement of Kolmogorov's inequality.

Application: Brownian motion

Let B denote canonical one-dimensional Brownian motion. Then

The proof is just as follows: since the exponential function is monotonically increasing, for any non-negative λ,

By Doob's inequality, and since the exponential of Brownian motion is a positive submartingale,

Since the left-hand side does not depend on λ, choose λ to minimize the right-hand side: λ = C/T gives the desired inequality.

References

{{cite book |author1=Revuz, Daniel |author2=Yor, Marc | title=Continuous martingales and Brownian motion | edition=Third | publisher=Springer| location=Berlin | year=1999 | isbn=3-540-64325-7}} (Theorem II.1.7)
{{springer|id=M/m062570|title=Martingale|author=Shiryaev, Albert N.}}

3 : Probabilistic inequalities|Statistical inequalities|Martingale theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。