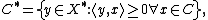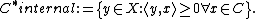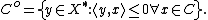请输入您要查询的百科知识：

　

词条 Dual cone and polar cone
释义

  1. Dual cone

  2. Self-dual cones

  3. Polar cone

  4. See also

  5. References

Dual cone and polar cone are closely related concepts in convex analysis, a branch of mathematics.

Dual cone

The dual cone C{{sup|*}} of a subset C in a linear space X, e.g. Euclidean space Rn, with topological dual space X{{sup|*}} is the set

where 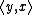is the duality pairing between X and X{{sup|*}}, i.e. .

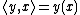C{{sup|*}} is always a convex cone, even if C is neither convex nor a cone.

Alternatively, many authors define the dual cone in the context of a real Hilbert space (such as Rn equipped with the Euclidean inner product) to be what is sometimes called the internal dual cone.

Using this latter definition for C{{sup|*}}, we have that when C is a cone, the following properties hold:[1]

  • A non-zero vector y is in C{{sup|}} if and only if both of the following conditions hold:
    1. y is a normal at the origin of a hyperplane that supports C.
    2. y and C lie on the same side of that supporting hyperplane.
    3. C{{sup|}} is closed and convex.
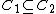    4. implies .
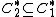    5. If C has nonempty interior, then C{{sup|}} is pointed, i.e. C contains no line in its entirety.
    6. If C is a cone and the closure of C is pointed, then C{{sup|}} has nonempty interior.
    7. C{{sup|}} is the closure of the smallest convex cone containing C (a consequence of the hyperplane separation theorem)

Self-dual cones

A cone C in a vector space X is said to be self-dual if X can be equipped with an inner product ⟨⋅,⋅⟩ such that the internal dual cone relative to this inner product is equal to C.[2] Those authors who define the dual cone as the internal dual cone in a real Hilbert space usually say that a cone is self-dual if it is equal to its internal dual. This is slightly different than the above definition, which permits a change of inner product. For instance, the above definition makes a cone in Rn with ellipsoidal base self-dual, because the inner product can be changed to make the base spherical, and a cone with spherical base in Rn is equal to its internal dual.

The nonnegative orthant of Rn and the space of all positive semidefinite matrices are self-dual, as are the cones with ellipsoidal base (often called "spherical cones", "Lorentz cones", or sometimes "ice-cream cones"). So are all cones in R3 whose base is the convex hull of a regular polygon with an odd number of vertices. A less regular example is the cone in R3 whose base is the "house": the convex hull of a square and a point outside the square forming an equilateral triangle (of the appropriate height) with one of the sides of the square.

Polar cone

For a set C in X, the polar cone of C is the set[3]

It can be seen that the polar cone is equal to the negative of the dual cone, i.e. Co = −C{{sup|*}}.

For a closed convex cone C in X, the polar cone is equivalent to the polar set for C.[4]

See also

  • Bipolar theorem
  • Polar set

References

1. ^{{cite book|title=Convex Optimization | first1=Stephen P. |last1=Boyd |first2=Lieven|last2=Vandenberghe|year=2004|publisher=Cambridge University Press|isbn=978-0-521-83378-3 | url=http://www.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf |format=pdf|accessdate=October 15, 2011|pages=51–53}}
2. ^Iochum, Bruno, "Cônes autopolaires et algèbres de Jordan", Springer, 1984.
3. ^{{cite book|author=Rockafellar, R. Tyrrell|title=Convex Analysis | publisher=Princeton University Press |location=Princeton, NJ|year=1997|origyear=1970|isbn=978-0-691-01586-6|pages=121–122}}
4. ^{{cite book|last=Aliprantis |first=C.D.|last2=Border |first2=K.C. |title=Infinite Dimensional Analysis: A Hitchhiker's Guide|edition=3|publisher=Springer|year=2007|isbn=978-3-540-32696-0|doi=10.1007/3-540-29587-9|page=215}}
  • {{cite book

| last = Goh
| first = C. J.
|author2=Yang, X.Q.
| title = Duality in optimization and variational inequalities
| publisher = London; New York: Taylor & Francis
| year = 2002
| pages =
| isbn = 0-415-27479-6
}}
  • {{cite book

| last = Boltyanski
| first = V. G.
| authorlink= Vladimir Boltyansky
|author2=Martini, H. |author3=Soltan, P.
| title = Excursions into combinatorial geometry
| publisher = New York: Springer
| year = 1997
| pages =
| isbn = 3-540-61341-2
}}
  • {{cite book

| last = Ramm
| first = A.G.
|editor=Shivakumar, P.N. |editor2=Strauss, A.V.
| title = Operator theory and its applications
| publisher = Providence, R.I.: American Mathematical Society
| year = 2000
| pages =
| isbn = 0-8218-1990-9
}}

3 : Convex geometry|Linear programming|Convex analysis
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/14 5:44:06