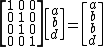“Duplication and elimination matrices”的意思、由来-开放百科全书

词条

Duplication and elimination matrices

释义

Duplication matrix
Elimination matrix
Notes
References

In mathematics, especially in linear algebra and matrix theory, the duplication matrix and the elimination matrix are linear transformations used for transforming half-vectorizations of matrices into vectorizations or (respectively) vice versa.

Duplication matrix

The duplication matrix D_n is the unique n² × n(n+1)/2 matrix which, for any n × n symmetric matrix A, transforms vech(A) into vec(A):

D_n vech(A) = vec(A).

For the 2×2 symmetric matrix A = 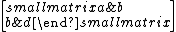, this transformation reads

Elimination matrix

An elimination matrix L_n is a n(n+1)/2 × n² matrix which, for any n × n matrix A, transforms vec(A) into vech(A):

L_n vec(A) = vech(A). ^[1]

For the 2×2 matrix A = , one choice for this transformation is given by

.

Notes

1. ^{{harvtxt|Magnus|Neudecker|1980}}, Definition 3.1

References

{{Citation | last1=Magnus | first1=Jan R. | last2=Neudecker | first2=Heinz | title=The elimination matrix: some lemmas and applications | doi=10.1137/0601049 | year=1980 | journal=Society for Industrial and Applied Mathematics. Journal on Algebraic and Discrete Methods | issn=0196-5212 | volume=1 | issue=4 | pages=422–449| url=http://repository.uvt.nl/id/ir-uvt-nl:oai:wo.uvt.nl:153210 }}.
Jan R. Magnus and Heinz Neudecker (1988), Matrix Differential Calculus with Applications in Statistics and Econometrics, Wiley. {{ISBN|0-471-98633-X}}.
Jan R. Magnus (1988), Linear Structures, Oxford University Press. {{ISBN|0-19-520655-X}}

Eliminationsmatrix

1 : Matrices

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。