微分在近似计算上的应用weffen zai jinsi jisuan shangde yingyong

设f (x)是可微函数. 由于当|△x|很小时，函数的改变量与微分之差| △y-dy|比|△x|小得多，而dy又比△y容易计算，所以用dy近似代替△y是有实际意义的.
可用微分解决以下两类近似计算问题：
❶利用公式

△y =f(x₀ +△x)-f(x₀)≈f′(x₀)△x

计算函数改变量的近似值.

❷利用公式

f (x₀ +△x)≈f(x₀)+f′ (x₀)△x

或

f(x)≈f(x₀)+f′ (x₀) (x -x₀)　(1)

计算函数值的近似值.
用微分作上述的近似计算，首先要根据问题的需要确定函数f (x)；然后恰当地选择x₀与△x的值，使得f (x₀),f ′ (x₀)容易计算，且|△x|尽可能小.
例 求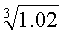的近似值.
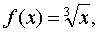解 可取x₀＝ 1,△x= 0. 02. 于是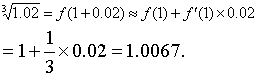

在式 (1) 中，令x₀＝0，得

f(x) ≈f(0)+f′ (0)x　(2)

当|x|充分小时，可由式(2)推出几个常用的近似公式，如

sinx ≈x,tgx ≈ x,1n (1 +x) ≈x