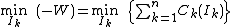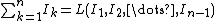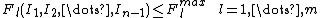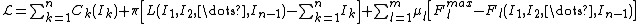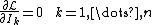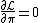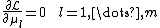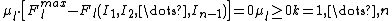“Economic dispatch”的意思、由来-开放百科全书

The main idea is that, in order to satisfy the load at a minimum total cost, the set of generators with the lowest marginal costs must be used first, with the marginal cost of the final generator needed to meet load setting the system marginal cost. This is the cost of delivering one additional MWh of energy onto the system. The historic methodology for economic dispatch was developed to manage fossil fuel burning power plants, relying on calculations involving the input/output characteristics of power stations.

Basic mathematical formulation

The following is based on Kirschen (2010).^[2] The economic dispatch problem can be thought of as maximising the economic welfare {{math|W}} of a power network whilst meeting system constraints. For a network with {{math|n}} buses (nodes), where {{math|I_k}} represents the net power injection at bus {{math|k}}, and {{math|C_k(I_k)}} is the cost function of producing power at bus {{math|k}}, the unconstrained problem is formulated as:

Constraints imposed on the model are the need to maintain a power balance, and that the flow on any line must not exceed its capacity. For the power balance, the sum of the net injections at all buses must be equal to the power losses in the branches of the network:

The power losses {{math|L}} depend on the flows in the branches and thus on the net injections as shown in the above equation. However it cannot depend on the injections on all the buses as this would give an over-determined system. Thus one bus is chosen as the Slack bus and is omitted from the variables of the function {{math|L}}. The choice of Slack bus is entirely arbitrary, here bus {{math|n}} is chosen.

The second constraint involves capacity constraints on the flow on network lines. For a system with {{math|m}} lines this constraint is modeled as:

where {{math|F_l}} is the flow on branch {{math|l}}, and {{math|F_l^max}} is the maximum value that this flow is allowed to take. Note that the net injection at the slack bus is not included in this equation for the same reasons as above.

These equations can now be combined to build the Lagrangian of the optimization problem:

where π and μ are the Lagrangian multipliers of the constraints. The conditions for optimality are then:

where the last condition is needed to handle the inequality constraint on line capacity.

Solving these equations is computationally difficult as they are nonlinear and implicitly involve the solution of the power flow equations. The analysis can be simplified using a linearised model called a DC power flow.

Environmental dispatch

In environmental dispatch, additional considerations concerning reduction of pollution further complicate the power dispatch problem. The basic constraints of the economic dispatch problem remain in place but the model is optimized to minimize pollutant emission in addition to minimizing fuel costs and total power loss.^[3] Due to the added complexity, a number of algorithms have been employed to optimize this environmental/economic dispatch problem. Notably, a modified bees algorithm implementing chaotic modeling principles was successfully applied not only in silico, but also on a physical model system of generators.^[3]. Other methods used to address the economic emission dispatch problem include Particle Swarm Optimization (PSO) and neural networks ^[6]

Another notable algorithm combination is used in a real-time emissions tool called Locational Emissions Estimation Methodology (LEEM) that links electric power consumption and the resulting pollutant emissions.^[4] The LEEM estimates changes in emissions associated with incremental changes in power demand derived from the locational marginal price (LMP) information from the independent system operators (ISOs) and emissions data from the US Environmental Protection Agency (EPA).^[4] LEEM was developed at Wayne State University as part of a project aimed at optimizing water transmission systems in Detroit, MI starting in 2010 and has since found a wider application as a load profile management tool that can help reduce generation costs and emissions.^[5]

See also

References

1. ^[https://web.archive.org/web/20110429035824/http://www.doi.gov/pam/EnergyPolicyAct2005.pdf Energy Policy Act 2005].
2. ^{{cite book|last=Kirschen|first=Daniel|title=Fundamentals of Power System Economics|year=2010|publisher=Wiley|isbn=978-0-470-84572-1}}
3. ^¹{{cite journal|last1=Morsali|first1=Roozbeh|last2=Mohammadi|first2=Mohsen|last3=Maleksaeedi|first3=Iman|last4=Ghadimi|first4=Noradin|title=A new multiobjective procedure for solving nonconvex environmental/economic power dispatch|journal=Complexity|volume=20|issue=2|pages=47–62|doi=10.1002/cplx.21505|bibcode=2014Cmplx..20b..47M|year=2014}}
4. ^¹{{cite book|last1=Carter|first1=TH|last2=Wang|first2=C|last3=Miller|first3=SS|last4=McEllmurry|first4=SP|last5=Miller|first5=CJ|last6=Hutt|first6=IA|title=Modeling of power generation pollutant emissions based on locational marginal prices for sustainable water delivery|journal=Energytech, 2011 IEEE|pages=1, 6, 25–26|doi=10.1109/EnergyTech.2011.5948499|url=http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=5948499&isnumber=5948497|year=2011|isbn=978-1-4577-0777-3}}
5. ^{{cite book|last1=Wang|first1=C|last2=McEllmurry|first2=SP|last3=Miller|first3=CJ|last4=Zhou|first4=J|title=An integrated economic/emission/ load profile management dispatch algorithm|journal=IEEE PES General Meeting 2012|pages=25–26|doi=10.1109/PESGM.2012.6345405|year=2012|isbn=978-1-4673-2729-9}}
6. ^¹{{cite book|last=Mason|first=Karl|author2=Duggan, Jim|author3=Howley, Enda|title=Evolving Multi-objective Neural Networks Using Differential Evolution for Dynamic Economic Emission Dispatch|journal=Proceedings of the Genetic and Evolutionary Computation Conference Companion|year=2017|volume=2017|pages=1287–1294|doi =10.1145/3067695.3082480|isbn=9781450349390}}

Basic mathematical formulation

Environmental dispatch

See also

References

External links