“Edge cover”的意思、由来-开放百科全书

词条

Edge cover

释义

Definition
Examples
Algorithms
See also
Notes
References

In graph theory, an edge cover of a graph is a set of edges such that every vertex of the graph is incident to at least one edge of the set.

In computer science, the minimum edge cover problem is the problem of finding an edge cover of minimum size. It is an optimization problem that belongs to the class of covering problems and can be solved in polynomial time.

Definition

Formally, an edge cover of a graph G is a set of edges C such that each vertex in G is incident with at least one edge in C. The set C is said to cover the vertices of G. The following figure shows examples of edge coverings in two graphs.

A minimum edge covering is an edge covering of smallest possible size. The edge covering number 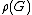is the size of a minimum edge covering. The following figure shows examples of minimum edge coverings.

Note that the figure on the right is not only an edge cover but also a matching. In particular, it is a perfect matching: a matching M in which each vertex is incident with exactly one edge in M. A perfect matching (if it exists) is always a minimum edge covering.

Examples

The set of all edges is an edge cover, assuming that there are no degree-0 vertices.
The complete bipartite graph K_m,n has edge covering number max(m, n).

Algorithms

A smallest edge cover can be found in polynomial time by finding a maximum matching and extending it greedily so that all vertices are covered.^[1]^[1] In the following figure, a maximum matching is marked with red; the extra edges that were added to cover unmatched nodes are marked with blue. (The figure on the right shows a graph in which a maximum matching is a perfect matching; hence it already covers all vertices and no extra edges were needed.)

On the other hand, the related problem of finding a smallest vertex cover is an NP-hard problem.^[2]

Notes

1. ^{{citation|title=Combinatorial optimization: networks and matroids|first=Eugene L.|last=Lawler|publisher=Dover Publications|year=2001|isbn=978-0-486-41453-9|pages=222–223|url=https://books.google.com/books?id=m4MvtFenVjEC&pg=PA222}}.
2. ^¹{{harvtxt|Garey|Johnson|1979}}, p. 79, uses edge cover and vertex cover as one example of a pair of similar problems, one of which can be solved in polynomial time while the other one is NP-hard. See also p. 190.

References

{{MathWorld|urlname=EdgeCover|title=Edge Cover}}
{{citation

}}.

2 : Computational problems in graph theory|Polynomial-time problems

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。