“Edmonds matrix”的意思、由来-开放百科全书

词条

Edmonds matrix

释义

References

In graph theory, the Edmonds matrix of a balanced bipartite graph with sets of vertices and is defined by

where the x_ij are indeterminates. One application of the Edmonds matrix of a bipartite graph is that the graph admits a perfect matching if and only if the polynomial det(A_ij) in the x_ij is not identically zero. Furthermore, the number of perfect matchings is equal to the number of monomials in the polynomial det(A), and is also equal to the permanent of . In addition, rank of is equal to the maximum matching size of .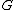

The Edmonds matrix is named after Jack Edmonds. The Tutte matrix is a generalisation to non-bipartite graphs.

References

{{cite book|author=R. Motwani, P. Raghavan |title=Randomized Algorithms |url=https://books.google.com/?id=QKVY4mDivBEC&pg=PR5#PPA167,M1 |publisher=Cambridge University Press|year=1995|page=167|isbn=9780521474658 }}
{{cite book|author=Allen B. Tucker|title=Computer Science Handbook|publisher=CRC Press|date=2004|isbn=1-58488-360-X|page=12.19}}

1 : Algebraic graph theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。