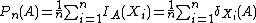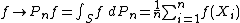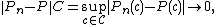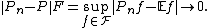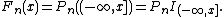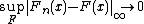- Definition
- Empirical distribution function
- See also
- References
- Further reading
In probability theory, an empirical measure is a random measure arising from a particular realization of a (usually finite) sequence of random variables. The precise definition is found below. Empirical measures are relevant to mathematical statistics.
The motivation for studying empirical measures is that it is often impossible to know the true underlying probability measure  . We collect observations
. We collect observations 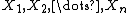 and compute relative frequencies. We can estimate
and compute relative frequencies. We can estimate  , or a related distribution function
, or a related distribution function  by means of the empirical measure or empirical distribution function, respectively. These are uniformly good estimates under certain conditions. Theorems in the area of empirical processes provide rates of this convergence.
by means of the empirical measure or empirical distribution function, respectively. These are uniformly good estimates under certain conditions. Theorems in the area of empirical processes provide rates of this convergence.
Definition
Let 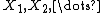 be a sequence of independent identically distributed random variables with values in the state space S with probability distribution P.
be a sequence of independent identically distributed random variables with values in the state space S with probability distribution P.
The empirical measure Pn is defined for measurable subsets of S and given by
Propertieswhereis the indicator function and
is the Dirac measure.
- For a fixed measurable set A, nPn(A) is a binomial random variable with mean nP(A) and variance nP(A)(1 − P(A)).
- In particular,Pn(A) is an unbiased estimator of P(A).
- For a fixed partition
 of S, random variables
of S, random variables 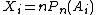 form a multinomial distribution with event probabilities
form a multinomial distribution with event probabilities 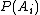
- The covariance matrix of this multinomial distribution is
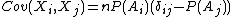 .
.
- The covariance matrix of this multinomial distribution is
is the empirical measure indexed by
, a collection of measurable subsets of S.
To generalize this notion further, observe that the empirical measure 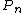 maps measurable functions
maps measurable functions 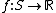 to their empirical mean,
to their empirical mean,
In particular, the empirical measure of A is simply the empirical mean of the indicator function, Pn(A) = Pn IA.
For a fixed measurable function  ,
, 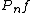 is a random variable with mean
is a random variable with mean 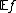 and variance
and variance 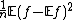 .
.
By the strong law of large numbers, Pn(A) converges to P(A) almost surely for fixed A. Similarly 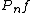 converges to
converges to 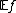 almost surely for a fixed measurable function
almost surely for a fixed measurable function  . The problem of uniform convergence of Pn to P was open until Vapnik and Chervonenkis solved it in 1968.[1]
. The problem of uniform convergence of Pn to P was open until Vapnik and Chervonenkis solved it in 1968.[1]
If the class  (or
(or  ) is Glivenko–Cantelli with respect to P then Pn converges to P uniformly over
) is Glivenko–Cantelli with respect to P then Pn converges to P uniformly over 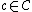 (or
(or 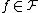 ). In other words, with probability 1 we have
). In other words, with probability 1 we have
Empirical distribution function
{{main|Empirical distribution function}}The empirical distribution function provides an example of empirical measures. For real-valued iid random variables  it is given by
it is given by
In this case, empirical measures are indexed by a class  It has been shown that
It has been shown that  is a uniform Glivenko–Cantelli class, in particular,
is a uniform Glivenko–Cantelli class, in particular,
with probability 1.
See also
- Poisson random measure
References
Further reading
- {{cite book |first=P. |last=Billingsley |title=Probability and Measure |publisher=John Wiley and Sons |location=New York |edition=Third |year=1995 |isbn=0-471-80478-9 }}
- {{cite journal |first=M. D. |last=Donsker |title=Justification and extension of Doob's heuristic approach to the Kolmogorov–Smirnov theorems |journal=Annals of Mathematical Statistics |volume=23 |issue=2 |pages=277–281 |year=1952 |doi=10.1214/aoms/1177729445 }}
- {{cite journal |first=R. M. |last=Dudley |title=Central limit theorems for empirical measures |journal=Annals of Probability |volume=6 |issue=6 |pages=899–929 |year=1978 |jstor=2243028 |doi=10.1214/aop/1176995384}}
- {{cite book |first=R. M. |last=Dudley |title=Uniform Central Limit Theorems |series=Cambridge Studies in Advanced Mathematics |volume=63 |publisher=Cambridge University Press |location=Cambridge, UK |year=1999 |isbn=0-521-46102-2 }}
- {{cite journal |first=J. |last=Wolfowitz |title=Generalization of the theorem of Glivenko–Cantelli |journal=Annals of Mathematical Statistics |volume=25 |issue=1 |pages=131–138 |year=1954 |jstor=2236518 |doi=10.1214/aoms/1177728852}}
- 12 step fellowships
- 12 step program
- 12 Steps Saga
- 12 step treatment
- 12 Stops and Home
- 12 Stories Down
- 12 (Street Fighter)
- 12-string
- 12 string
- 12-String Blues
- 12 String Guitar
- 12 Super Éxitos
- 12 tables
- 12TET
- 12th Academy Awards
- 12th Aero Squadron
- 12th Air Base
- 12th Air Division
- 12th Air Force
- 12th Alpini Regiment
- 12th Amendment to the U.S. Constitution
- 12th American Music Awards
- 12th Annual Interactive Fiction Competition 2006
- 12th Archeological Conference
- 12th Archeological Congress