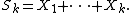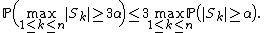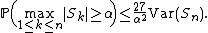“Etemadi's inequality”的意思、由来-开放百科全书

词条

Etemadi's inequality

释义

Statement of the inequality
Remark
References

In probability theory, Etemadi's inequality is a so-called "maximal inequality", an inequality that gives a bound on the probability that the partial sums of a finite collection of independent random variables exceed some specified bound. The result is due to Nasrollah Etemadi.

Statement of the inequality

Let X₁, ..., X_n be independent real-valued random variables defined on some common probability space, and let α ≥ 0. Let S_k denote the partial sum

Then

Remark

Suppose that the random variables X_k have common expected value zero. Apply Chebyshev's inequality to the right-hand side of Etemadi's inequality and replace α by α / 3. The result is Kolmogorov's inequality with an extra factor of 27 on the right-hand side:

References

{{cite book | last=Billingsley | first=Patrick | title=Probability and Measure | publisher=John Wiley & Sons, Inc. | location=New York | year=1995 | isbn=0-471-00710-2}} (Theorem 22.5)
{{cite journal | last=Etemadi | first=Nasrollah | title=On some classical results in probability theory | journal=Sankhyā Ser. A | volume=47 | year=1985 | pages=215–221 |mr=0844022 | jstor = 25050536 | issue=2 }}

2 : Probabilistic inequalities|Statistical inequalities

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。