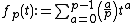- References
- External links
In mathematics, a Fekete polynomial is a polynomial
where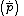 
is the Legendre symbol modulo some integer p > 1.
These polynomials were known in nineteenth-century studies of Dirichlet L-functions, and indeed to Peter Gustav Lejeune Dirichlet himself. They have acquired the name of Michael Fekete, who observed that the absence of real zeroes t of the Fekete polynomial with 0 < t < 1 implies an absence of the same kind for the L-function
This is of considerable potential interest in number theory, in connection with the hypothetical Siegel zero near s = 1. While numerical results for small cases had indicated that there were few such real zeroes, further analysis reveals that this may indeed be a 'small number' effect.
References
- Peter Borwein: Computational excursions in analysis and number theory. Springer, 2002, {{ISBN|0-387-95444-9}}, Chap.5.
External links
- Brian Conrey, Andrew Granville, Bjorn Poonen and Kannan Soundararajan, [https://arxiv.org/abs/math/9906214v1 Zeros of Fekete polynomials], arXiv e-print math.NT/9906214, June 16, 1999.
2 : Polynomials|Zeta and L-functions
- Sandra Bacon
- Sandra Beavis
- Sandra Beech
- Sandra Bell-Lundy
- Sandra Beltran
- Sandra Bem
- Sandra Benes
- Sandra Bernhardt
- Sandra Bertrand
- Sandra Bezic
- Sandra Binion
- Sandra Birch Lee
- Sandra "Blue" Good
- Sandra Bolden Cunningham
- Sandra Bookman
- Sandra Botha
- Sandra Bradshaw
- Sandra Brand
- Sandra Briggs
- Sandra Brown
- Sandra Brown (campaigner)
- Sandra Brown, OBE
- Sandra Caldarone
- Sandra Castillo
- Sandra Chambers