“Fiber derivative”的意思、由来-开放百科全书

词条

Fiber derivative

释义

References

{{multiple issues|{{Orphan|date=February 2013}}{{unreferenced|date=August 2012}}
}}

In the context of Lagrangian Mechanics the fiber derivative is used to convert between the Lagrangian and Hamiltonian forms. In particular, if is the configuration manifold then the Lagrangian is defined on the tangent bundle 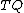and the Hamiltonian is defined on the cotangent bundle 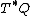—the fiber derivative is a map 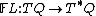such that

,

where and are vectors from the same tangent space. When restricted to a particular point, the fiber derivative is a Legendre transformation.

References

Marsden, Jerrod E.; Ratiu, Tudor (1998). Introduction to Mechanics and Symmetry: A Basic Exposition of Classical Mechanical Systems

1 : Lagrangian mechanics

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。