抽样分布chouyang fenbu
指在众多的样本中某种统计量(如平均数或标准差)的分布。如在一个总体中抽取n=30的许多个样本,一个样本就有一个平均数,这许多样本的平均数的分布,就是一种抽样分布。
抽样分布有几个定理:若在总体中抽取容量为n的一切样本,则:❶样本平均数的平均(μx)等于总体平均数,即: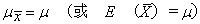
式中 ——样本平均数
μ——总体平均数
E——期望值(或所有统计量的平均值)
❷样本平均数的标准差(S)等于总体标准差除以n的方根,即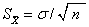
式中 σ——总体的标准差
n——样本容量
显然,亦有Sx2=δ2/n。
❸当n为大样本(如n≥30)时,样本平均数的分布近似于正态分布。
由定理
❸可知:当总体分布为正态时,样本平均数的分布也是正态的;当总体分布不是正态时,样本平均数的分布仍趋于正态,而且样本容量愈大,样本平均数的分布愈接近于正态。
上述定理在统计推断中有重要应用。
抽样分布sampling distribution
样本统计量的概率分布。它是样本推断总体的理论基础。按随机抽样方式从总体抽取一定容量的所有可能的样本,样本统计量如平均数,方差S2,t值等等将形成特定的概率分布。农业化学研究中常用的抽样分布有如下几种:
样本平均数的分布 如果从平均数为μ,方差为σ2的总体X中随机抽取容量为n的样本:x1,x2,…,xn,则样本平均数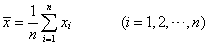
其分布性质为:❶μ=μ (μ为样本平均数分布的数学期望);
❷σ2=σ2/n)(σ2为样本平均数分布的方差);
❸如果x~N(μ,σ2),则~N(μ,σ2/n);
❹如果母总体X具有平均数μ,方差σ2,但分布不呈正态或分布形式未知,则随样本容量n的增大,样本平均数的分布渐趋于正态分布。
样本平均数差数的分布 如果从平均数为μ1,方差为σ12的总体X1中随机抽取容量为n1的所有可能样

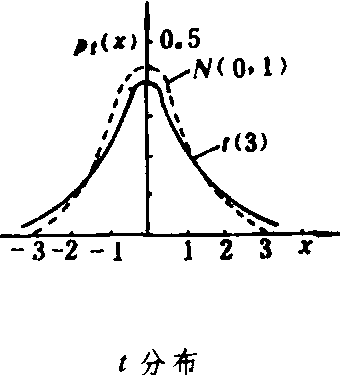
χ2分布 从一个平均数μ和方差σ2已知的正态总体X中随机抽取容量为n的样本,x1,x2,…,xn,则统计量χ2定义为
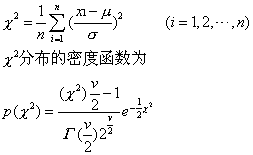
式中 v为自由度等于n。如果总体平均数μ未知,则

线倾斜,且随自由度减小倾斜度加剧。X2的定义域为(0,∞)。实际上任一统计量只要其密度函数与p(X2)相符都是具有X2分布的统计量。
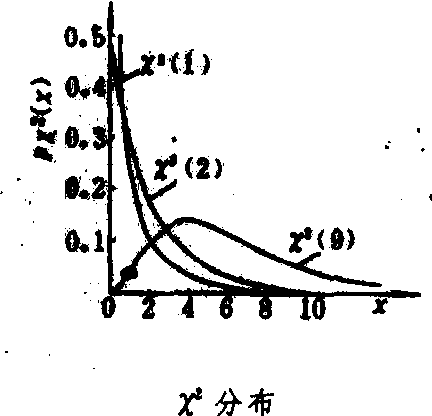

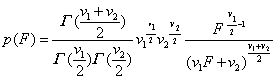
式中 v1和v2分别为F的分子S21和分母S22的自由度,是p(F)的两个参数。F分布的定义域(0,∞),F分布曲线是随v1和v2不同而异的一组曲线,通常是偏斜的(见图)。
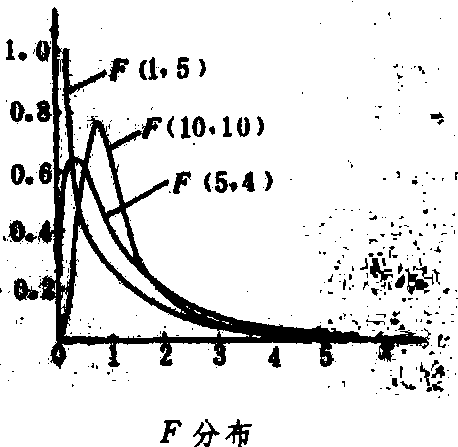
抽样分布
统计量的分布。常被应用于测验分数统计中。
抽样分布sampling distribution
又称样本分布。全称随机抽样分布(random sampling distribution)。从一个总体中,按一定的样本容量,随机地抽出全部所有可能的样本,由每个样本计算出的某一个统计数所组成的一种分布。例如在一个平均数为μ,方差为σ2的正态总体中抽祥,样本容量为n,则每个样本可以得到一个样本平均数 i。当抽出全部所有可能的样本后,则这些
i。当抽出全部所有可能的样本后,则这些 i也可组成一个新的正态分布。 其参数
i也可组成一个新的正态分布。 其参数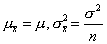 。这里,μ
。这里,μ 和
和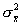 分别为平均数抽样分布总体的平均数和方差。
分别为平均数抽样分布总体的平均数和方差。