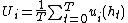- Preliminaries
- Infinitely-repeated games without discounting Subgame perfection Overtaking
- Infinitely-repeated games with discounting Subgame perfection
- Finitely-repeated games without discount
- Applications
- Summary of folk theorems
- Notes
- References
name= Folk theorem|
subsetof = Minimax, Nash Equilibrium|
discoverer = various, notably Ariel Rubinstein|
usedfor = repeated games|
example = Repeated prisoner's dilemma}}
In game theory, folk theorems are a class of theorems about possible Nash equilibrium payoff profiles in repeated games {{harv|Friedman|1971}}.[1] The original Folk Theorem concerned the payoffs of all the Nash equilibria of an infinitely repeated game. This result was called the Folk Theorem because it was widely known among game theorists in the 1950s, even though no one had published it. Friedman's (1971) Theorem concerns the payoffs of certain subgame-perfect Nash equilibria (SPE) of an infinitely repeated game, and so strengthens the original Folk Theorem by using a stronger equilibrium concept subgame-perfect Nash equilibria rather than Nash equilibrium.[2]
The Folk Theorem suggests that if the player is patient enough and far-sighted (i.e. if discount factor  ) then not only can repeated interaction allow many SPE outcomes, but actually SPE can allow virtually any outcome in the sense of average payoffs. Put more simply, the theorem suggests that anything that is feasible and individually rational is possible.[3]
) then not only can repeated interaction allow many SPE outcomes, but actually SPE can allow virtually any outcome in the sense of average payoffs. Put more simply, the theorem suggests that anything that is feasible and individually rational is possible.[3]
For example, in the one-shot Prisoner's Dilemma, if both players cooperate that is not a Nash equilibrium. The only Nash equilibrium is that both players defect, which is also a mutual minmax profile. One folk theorem says that, in the infinitely repeated version of the game, provided players are sufficiently patient, there is a Nash equilibrium such that both players cooperate on the equilibrium path. But in finitely repeated game by using backward induction it can be determined that players play Nash equilibrium in the last period of the game (which is to defect).
Preliminaries
Any Nash equilibrium payoff in a repeated game must satisfy two properties:
1. Individual rationality (IR): the payoff must weakly dominate the minmax payoff profile of the constituent stage game. That is, the equilibrium payoff of each player must be at least as large as the minmax payoff of that player. This is because a player achieving less than his minmax payoff always has incentive to deviate by simply playing his minmax strategy at every history.
2. Feasibility: the payoff must be a convex combination of possible payoff profiles of the stage game. This is because the payoff in a repeated game is just a weighted average of payoffs in the basic games.
Folk theorems are partially converse claims: they say that, under certain conditions (which are different in each folk theorem), every payoff that is both IR and feasible can be realized as a Nash equilibrium payoff profile in the repeated game.
There are various folk theorems; some relate to finitely-repeated games while others relate to infinitely-repeated games.[4]
Infinitely-repeated games without discounting
In the undiscounted model, the players are patient. They don't differentiate between utilities in different time periods. Hence, their utility in the repeated game is represented by the sum of utilities in the basic games.
When the game is infinite, a common model for the utility in the infinitely-repeated game is the infimum of the limit of means. If game results in a path of outcomes 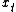 , player is utility is:
, player is utility is:
where  is the basic-game utility function of player i.
is the basic-game utility function of player i.
An infinitely-repeated game without discounting is often called a "supergame".
The folk theorem in this case is very simple and contains no pre-conditions: every IR feasible payoff profile in the basic game is an equilibrium payoff profile in the repeated game.
The proof employs what is called grim[5] or grim trigger[6] strategy. All players start by playing the prescribed action and continue to do so until someone deviates. If player i deviates, all players switch to the strategy which minmaxes player i forever after. The one-stage gain from deviation contributes 0 to the total utility of the player. The utility of a deviating player cannot be higher than his minmax payoff. Hence all players stay on the intended path.
Subgame perfection
The above Nash equilibrium is not always subgame perfect. If punishment is costly for the punishers, the threat of punishment is not credible.
A subgame perfect equilibrium requires a slightly more complicated strategy.[5][6]{{rp|146–149}} The punishment should not last forever; it should last only a finite time which is sufficient to wipe out the gains from deviation. After that, the other players should return to the equilibrium path.
The limit-of-means criterion ensures that any finite-time punishment has no effect on the final outcome. Hence, limited-time punishment is a subgame-perfect equilibrium.
- Coalition subgame-perfect equilibria:[9] An equilibrium is called a coalition Nash equilibrium if no coalition can gain from deviating. It is called a coalition subgame-perfect equilibrium if no coalition can gain from deviating after any history.[7] With the limit-of-means criterion, an outcome is attainable in coalition-Nash-equilibrium or in coalition-subgame-perfect-equilibrium, if-and-only-if it is Pareto efficient and weakly-coalition-individually-rational.[8]
Overtaking
Some authors claim that the limit-of-means criterion is unrealistic, because it implies that utilities in any finite time-span contribute 0 to the total utility. However, if the utilities in any finite time-span contribute a positive value, and the value is undiscounted, then it is impossible to attribute a finite numeric utility to an infinite outcome sequence. A possible solution to this problem is that, instead of defining a numeric utility for each infinite outcome sequence, we just define the preference relation between two infinite sequences. We say that agent  (strictly) prefers the sequence of outcomes
(strictly) prefers the sequence of outcomes  over the sequence
over the sequence 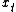 , if:[9][6]{{rp|139}}[10]
, if:[9][6]{{rp|139}}[10]
For example, consider the sequences  and
and 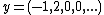 . According to the limit-of-means criterion, they are equivalent but according to the overtaking criterion,
. According to the limit-of-means criterion, they are equivalent but according to the overtaking criterion,  is better than
is better than  . See overtaking criterion for more information.
. See overtaking criterion for more information.
The folk theorems with the overtaking criterion are slightly weaker than with the limit-of-means criterion. Only outcomes that are strictly individually rational, can be attained in Nash equilibrium. This is because, if an agent deviates, he gains in the short run, and this gain can be wiped out only if the punishment gives the deviator strictly less utility than the agreement path. The following folk theorems are known for the overtaking criterion:
- Strict stationary equilibria:[9] A Nash equilibrium is called strict if each player strictly prefers the infinite sequence of outcomes attained in equilibrium, over any other sequence he can deviate to. A Nash equilibrium is called stationary if the outcome is the same in each time-period. An outcome is attainable in strict-stationary-equilibrium if-and-only-if for every player the outcome is strictly better than the player's minimax outcome.[11]
- Strict stationary subgame-perfect equilibria:[9] An outcome is attainable in strict-stationary-subgame-perfect-equilibrium, if for every player the outcome is strictly better than the player's minimax outcome (note that this is not an "if-and-only-if" result). To achieve subgame-perfect equilibrium with the overtaking criterion, it is required to punish not only the player that deviates from the agreement path, but also every player that does not cooperate in punishing the deviant.[6]{{rp|149–150}}
- The "stationary equilibrium" concept can be generalized to a "periodic equilibrium", in which a finite number of outcomes is repeated periodically, and the payoff in a period is the arithmetic mean of the payoffs in the outcomes. That mean payoff should be strictly above the minimax payoff.[9]
- Strict stationary coalition equilibria:[10] With the overtaking criterion, if an outcome is attainable in coalition-Nash-equilibrium, then it is Pareto efficient and weakly-coalition-individually-rational. On the other hand, if it is Pareto efficient and strongly-coalition-individually-rational[12] it can be attained in strict-stationary-coalition-equilibrium.
Infinitely-repeated games with discounting
Assume that the payoff of a player in an infinitely repeated game is given by the average discounted criterion with discount factor 0<δ<1:
The discount factor indicates how patient the players are.
The folk theorem in this case requires that the payoff profile in the repeated game strictly dominates the minmax payoff profile (i.e., each player receives strictly more than the minmax payoff).
Let a be a pure strategy profile with payoff profile x which strictly dominates the minmax payoff profile. One can define a Nash equilibrium with x as resulting payoff profile as follows:
1. All players start by playing a and continue to play a if no deviation occurs.
2. If any one player, say player i, deviated, play the strategy profile m which minmaxes i forever after.
3. Ignore multilateral deviations.
If player i gets ε more than his minmax payoff each stage by following 1, then the potential loss from punishment is
If δ is close to 1, this outweighs any finite one-stage gain, making the strategy a Nash equilibrium.
An alternative statement of this folk theorem[4] allows the equilibrium payoff profile x to be any IR feasible payoff profile; it only requires there exists an IR feasible payoff profile x, which strictly dominates the minmax payoff profile. Then, the folk theorem guarantees that it is possible to approach x in equilibrium to any desired precision (for every ε there exists a Nash equilibrium where the payoff profile is a distance ε away from x).
Subgame perfection
Attaining a subgame perfect equilibrium in discounted games is more difficult than in undiscounted games. The cost of punishment does not vanish (as with the limit-of-means criterion).
It is not always possible to punish the non-punishers endlessly (as with the overtaking criterion) since the discount factor makes punishments far away in the future irrelevant for the present. Hence, a different approach is needed: the punishers should be rewarded.
This requires an additional assumption, that the set of feasible payoff profiles is full dimensional and the min-max profile lies in its interior. The strategy is as follows.
1. All players start by playing a and continue to play a if no deviation occurs.
2. If any one player, say player i, deviated, play the strategy profile m which minmaxes i for N periods. (Choose N and δ large enough so that no player has incentive to deviate from phase 1.)
3. If no players deviated from phase 2, all player j ≠ i gets rewarded ε above j's min-max forever after, while player i continues receiving his min-max. (Full-dimensionality and the interior assumption is needed here.)
4. If player j deviated from phase 2, all players restart phase 2 with j as target.
5. Ignore multilateral deviations.
Player j ≠ i now has no incentive to deviate from the punishment phase 2. This proves the subgame perfect folk theorem.
Finitely-repeated games without discount
Assume that the payoff of a player in an finitely repeated game is given by a simple arithmetic mean:
A folk theorem for this case has the following additional requirement:[4]
In the basic game, for every player i, there is a Nash-equilibriumthat is strictly better, for i, then his minmax payoff.
This requirement is stronger than the requirement for discounted infinite games, which is in turn stronger than the requirement for undiscounted infinite games.
This requirement is needed because of the last step. In the last step, the only stable outcome is a Nash-equilibrium in the basic game. Suppose a player i gains nothing from the Nash equilibrium (since it gives him only his minmax payoff). Then, there is no way to punish that player.
On the other hand, if for every player there is a basic equilibrium which is strictly better than minmax, a repeated-game equilibrium can be constructed in two phases:
- In the first phase, the players alternate strategies in the required frequencies to approximate the desired payoff profile.
- In the last phase, the players play the preferred equilibrium of each of the players in turn.
In the last phase, no player deviates since the actions are already a basic-game equilibrium. If an agent deviates in the first phase, he can be punished by minmaxing him in the last phase. If the game is sufficiently long, the effect of the last phase is negligible, so the equilibrium payoff approaches the desired profile.
Applications
Folk theorems can be applied to a diverse number of fields. For example:
- Anthropology: in a community where all behavior is well known, and where members of the community know that they will continue to have to deal with each other, then any pattern of behavior (traditions, taboos, etc.) may be sustained by social norms so long as the individuals of the community are better off remaining in the community than they would be leaving the community (the minimax condition).
- International politics: agreements between countries cannot be effectively enforced. They are kept, however, because relations between countries are long-term and countries can use "minimax strategies" against each other. This possibility often depends on the discount factor of the relevant countries. If a country is very impatient (pays little attention to future outcomes), then it may be difficult to punish it (or punish it in a credible way).[5]
On the other hand, MIT economist Franklin Fisher has noted that the folk theorem is not a positive theory.[13] In considering, for instance, oligopoly behavior, the folk theorem does not tell the economist what firms will do, but rather that cost and demand functions are not sufficient for a general theory of oligopoly, and the economists must include the context within which oligopolies operate in their theory.[13]
In 2007, Borgs et al. proved that, despite the folk theorem, in the general case computing the Nash equilibria for repeated games is not easier than computing the Nash equilibria for one-shot finite games, a problem which lies in the PPAD complexity class.[14] The practical consequence of this is that no efficient (polynomial-time) algorithm is known that computes the strategies required by folk theorems in the general case.
Summary of folk theorems
The following table compares various folk theorems in several aspects:
- Horizon – whether game is repeated Finitely or Infinitely many times.
- Utilities – whether the utility of a player in the repeated game is assumed to be an arithmetic mean or a discounted sum.
- Conditions on G (the basic game) – whether there are any technical conditions that should hold in the one-shot game in order for the theorem to work.
- Conditions on x (the target payoff vector) – whether the theorem works for any IR and feasible payoff vector, or only on a subset of these vectors.
- Equilibrium type – if all conditions are met, what kind of equilibrium is guaranteed by the theorem – Nash or Subgame-perfect?
- Punishment type – what kind of punishment strategy is used to deter players from deviating?
| Published by | Horizon | Utilities | Conditions on G | Conditions on x | Guarantee | Equilibrium type | Punishment type |
|---|---|---|---|---|---|---|---|
| Benoit& Krishna[15] | Finite (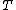 ) ) | Arithmetic mean | For every player there is an equilibrium payoff strictly better than minimax. | None | For all 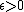 there is there is  such that, if such that, if  , for every , for every  there is equilibrium with payoff there is equilibrium with payoff  -close to -close to  . . | Nash | |
| Aumann& Shapley[5] | Infinite | Limit of means | None | None | Payoff exactly  . . | Nash | Grim |
| Aumann& Shapley[5] and Rubinstein[10][16] | Infinite | Limit of means | None | None | Payoff exactly  . . | Subgame-perfect | [6]{{rp>146–149}} |
| Rubinstein[9] | Infinite | Overtaking | None | Strictly above minimax. | Single outcome or a periodic sequence. | Subgame-perfect | [6]{{rp>149–150}} |
| Rubinstein[10] | Infinite | Limit of means | None | Pareto-efficient and weakly-coalition-individually-rational[8] | None | Coalition-subgame-perfect | |
| Rubinstein[10] | Infinite | Overtaking | None | Pareto-efficient and strongly-coalition-individually-rational[12] | None | Coalition-Nash | |
| Fudenberg& Maskin[17] | Infinite | Sum with discount  | Correlated mixed strategies are allowed. | Strictly above minimax. | When  is sufficiently near 1, there is an equilibrium with payoff exactly is sufficiently near 1, there is an equilibrium with payoff exactly  . . | Nash | Grim |
| Fudenberg& Maskin[17] | Infinite | Sum with discount  | Only pure strategies are allowed. | Strictly above minimax. | For all 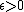 there is there is  such that, if such that, if  , for every , for every  there is an equilibrium with payoff there is an equilibrium with payoff  -close to -close to  . . | Nash | Grim punishment. |
| Friedman (1971,1977) | Infinite | Sum with discount  | Correlated mixed strategies are allowed. | Strictly above a Nash-equilibrium in G. | When  is sufficiently near 1, there is equilibrium with payoff exactly is sufficiently near 1, there is equilibrium with payoff exactly  . . | Subgame-perfect | Grim punishment using the Nash-equilibrium. |
| Fudenberg& Maskin[17] | Infinite | Sum with discount  | Two players | Strictly above minimax. | For all  there is there is  such that, if such that, if  , there is equilibrium with payoff exactly , there is equilibrium with payoff exactly  . . | Subgame-perfect | Limited-time punishment. |
| Fudenberg& Maskin[17] | Infinite | Sum with discount  | The IR feasible space is full-dimensional.[18] | Strictly above minimax. | For all  there is there is  such that, if such that, if  , there is equilibrium with payoff exactly , there is equilibrium with payoff exactly  . . | Subgame-perfect | [6]{{rp>150–153}} |
Notes
2. ^{{cite book |title= A Primer in Game Theory |authors= R. Gibbons |publisher=Harvester Wheatsheaf |isbn= 0-7450-1160-8 |year=1992|pages=89}}
3. ^{{cite web|url = http://web.stanford.edu/~jdlevin/Econ%20203/RepeatedGames.pdf |title= Bargaining and Repeated Games|author=Jonathan Levin| year = 2002}}
4. ^1 2 {{cite book |title=Game Theory |authors=Michael Maschler, Eilon Solan & Shmuel Zamir |publisher=Cambridge University Press |isbn=978-1-107-00548-8 |year=2013 |pages=176–180}}
5. ^1 2 3 4 {{cite book|doi=10.1007/978-1-4612-2648-2_1|chapter=Long-Term Competition—A Game-Theoretic Analysis|title=Essays in Game Theory|pages=1|year=1994|last1=Aumann|first1=Robert J.|last2=Shapley|first2=Lloyd S.|isbn=978-1-4612-7621-0}}
6. ^1 2 3 4 5 {{cite book|isbn=0-262-15041-7| ol=1084491M |lccn=94008308}}
7. ^The paper uses the term "strong equilibrium". Here, to prevent ambiguity, the term "coalition equilibrium" is used instead.
8. ^1 For every nonempty coalition
 , there is a strategy of the other players (
, there is a strategy of the other players ( ) such that for any strategy played by
) such that for any strategy played by  , the payoff when
, the payoff when  plays
plays 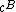 is not [strictly better for all members of
is not [strictly better for all members of  ].
].9. ^1 2 3 4 5 {{cite journal|doi= 10.1016/0022-0531(79)90002-4|title= Equilibrium in supergames with the overtaking criterion|journal= Journal of Economic Theory|volume= 21|pages= 1|year= 1979|last1= Rubinstein|first1= Ariel}}
10. ^1 2 3 4 5 {{cite journal|doi= 10.1007/BF01784792|title= Strong perfect equilibrium in supergames|journal= International Journal of Game Theory|volume= 9|pages= 1|year= 1980|last1= Rubinstein|first1= A.}}
11. ^In the 1979 paper, Rubinstein claims that an outcome is attainable in strict-stationary-equilibrium if-and-only-if for every player, the outcome is EITHER strictly better than the player's minimax outcome OR the outcome is weakly better than any other outcome the player can unilaterally deviate to. It is not clear how the second option is attainable in a strict equilibrium. In the 1994 book, this claim does not appear.
12. ^1 for every nonempty coalition
 , there is a strategy of the other players (
, there is a strategy of the other players ( ) such that for any strategy played by
) such that for any strategy played by  , the payoff is strictly worse for at least one member of
, the payoff is strictly worse for at least one member of  .
.13. ^1 Fisher, Franklin M. Games Economists Play: A Noncooperative View The RAND Journal of Economics, Vol. 20, No. 1. (Spring, 1989), pp. 113–124, this particular discussion is on page 118
14. ^{{cite web|url = http://research.microsoft.com/en-us/um/people/borgs/Papers/myth.pdf|title = The Myth of the Folk Theorem |author1=Christian Borgs |author2=Jennifer Chayes |author3=Nicole Immorlica |author4=Adam Tauman Kalai |author5=Vahab Mirrokni |author6=Christos Papadimitriou | year = 2007}}
15. ^{{cite journal|doi=10.2307/1912660|jstor=1912660|title=Finitely Repeated Games|journal=Econometrica|volume=53|issue=4|pages=905|year=1985|last1=Benoit|first1=Jean-Pierre|last2=Krishna|first2=Vijay}}
16. ^{{cite book|doi= 10.1007/978-1-4612-2648-2_2|chapter= Equilibrium in Supergames|title= Essays in Game Theory|pages= 17|year= 1994|last1= Rubinstein|first1= Ariel|isbn= 978-1-4612-7621-0}}
17. ^1 2 3 {{cite journal|doi= 10.2307/1911307|jstor= 1911307|title= The Folk Theorem in Repeated Games with Discounting or with Incomplete Information|journal= Econometrica|volume= 54|issue= 3|pages= 533|year= 1986|last1= Fudenberg|first1= Drew|last2= Maskin|first2= Eric|citeseerx= 10.1.1.308.5775}}
18. ^There is a collection of IR feasible outcomes
 , one per player, such that for every players
, one per player, such that for every players  ,
,  and
and  .
.References
- {{citation|last=Friedman|first=J.|year=1971|title=A non-cooperative equilibrium for supergames|journal=Review of Economic Studies|volume=38|pages=1–12|doi=10.2307/2296617|jstor=2296617|issue=1}}.
- Mas-Colell, A., Whinston, M and Green, J. (1995) Microeconomic Theory, Oxford University Press, New York (readable; suitable for advanced undergraduates.)
- Tirole, J. (1988) The Theory of Industrial Organization, MIT Press, Cambridge MA (An organized introduction to industrial organization)
- Ratliff, J. (1996). A Folk Theorem Sampler. A set of introductory notes to the Folk Theorem.
- Anthem (film)
- Anthem for a Lost Cause
- Anthem for the Unwanted
- Anthem (Goodness album)
- Anthem (Hanson album)
- Anthemic
- Anthem in
- Anthem Inc. (album)
- Anthem (insurance)
- Anthemions
- Anthemiopsis
- Anthemis abyssinica
- Anthemis ageratifolia
- Anthemis agrestis
- Anthemis anglica
- Anthemis artemisioides
- Anthemis australis
- Anthemis brachyglossa
- Anthemis brevifolia
- Anthemis bulgarica
- Anthemis buphthalmoides
- Anthemis carpatica
- Anthemis chrysantha
- Anthemis clavata
- Anthemis coarctata