“Formation matrix”的意思、由来-开放百科全书

词条

Formation matrix

释义

See also
Notes
References

In statistics and information theory, the expected formation matrix of a likelihood function 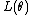is the matrix inverse of the Fisher information matrix of 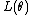, while the observed formation matrix of 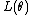is the inverse of the observed information matrix of 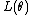.^[1]

Currently, no notation for dealing with formation matrices is widely used, but in books and articles by Ole E. Barndorff-Nielsen and Peter McCullagh, the symbol 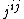is used to denote the element of the i-th line and j-th column of the observed formation matrix. The geometric interpretation of the Fisher information matrix (metric) leads to a notation of 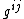following the notation of the (contravariant) metric tensor in differential geometry. The Fisher information metric is denoted by so that using Einstein notation we have .

These matrices appear naturally in the asymptotic expansion of the distribution of many statistics related to the likelihood ratio.

Notes

1. ^Edwards (1984) p104

References

Barndorff-Nielsen, O.E., Cox, D.R. (1989), Asymptotic Techniques for Use in Statistics, Chapman and Hall, London. {{ISBN|0-412-31400-2}}
Barndorff-Nielsen, O.E., Cox, D.R., (1994). Inference and Asymptotics. Chapman & Hall, London.
P. McCullagh, "Tensor Methods in Statistics", Monographs on Statistics and Applied Probability, Chapman and Hall, 1987.
Edwards, A.W.F. (1984) Likelihood. CUP. {{ISBN|0-521-31871-8}}

2 : Estimation theory|Information theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

See also

Notes

References