“Free Boolean algebra”的意思、由来-开放百科全书

词条

Free Boolean algebra

释义

A simple example
Category-theoretic definition
Topological realization
See also
References

In mathematics, a free Boolean algebra is a Boolean algebra with a distinguished set of elements, called generators, such that:

Each element of the Boolean algebra can be expressed as a finite combination of generators, using the Boolean operations, and
The generators are as independent as possible, in the sense that there are no relationships among them (again in terms of finite expressions using the Boolean operations) that do not hold in every Boolean algebra no matter which elements are chosen.

A simple example

The generators of a free Boolean algebra can represent independent propositions. Consider, for example, the propositions "John is tall" and "Mary is rich". These generate a Boolean algebra with four atoms, namely:

John is tall, and Mary is rich;
John is tall, and Mary is not rich;
John is not tall, and Mary is rich;
John is not tall, and Mary is not rich.

Other elements of the Boolean algebra are then logical disjunctions of the atoms, such as "John is tall and Mary is not rich, or John is not tall and Mary is rich". In addition there is one more element, FALSE, which can be thought of as the empty disjunction; that is, the disjunction of no atoms.

This example yields a Boolean algebra with 16 elements; in general, for finite n, the free Boolean algebra with n generators has 2ⁿ atoms, and therefore 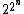elements.

If there are infinitely many generators, a similar situation prevails except that now there are no atoms. Each element of the Boolean algebra is a combination of finitely many of the generating propositions, with two such elements deemed identical if they are logically equivalent.

Category-theoretic definition

In the language of category theory, free Boolean algebras can be defined simply in terms of an adjunction between the category of sets and functions, Set, and the category of Boolean algebras and Boolean algebra homomorphisms, BA. In fact, this approach generalizes to any algebraic structure definable in the framework of universal algebra.

Above, we said that a free Boolean algebra is a Boolean algebra with a set of generators that behave a certain way; alternatively, one might start with a set and ask which algebra it generates. Every set X generates a free Boolean algebra FX defined as the algebra such that for every algebra B and function f : X → B, there is a unique Boolean algebra homomorphism f′ : FX → B that extends f. Diagrammatically,

where i_X is the inclusion, and the dashed arrow denotes uniqueness. The idea is that once one chooses where to send the elements of X, the laws for Boolean algebra homomorphisms determine where to send everything else in the free algebra FX. If FX contained elements inexpressible as combinations of elements of X, then f′ wouldn't be unique, and if the elements of X weren't sufficiently independent, then f′ wouldn't be well defined! It is easily shown that FX is unique (up to isomorphism), so this definition makes sense. It is also easily shown that a free Boolean algebra with generating set X, as defined originally, is isomorphic to FX, so the two definitions agree.

One shortcoming of the above definition is that the diagram doesn't capture that f′ is a homomorphism; since it is a diagram in Set each arrow denotes a mere function. We can fix this by separating it into two diagrams, one in BA and one in Set. To relate the two, we introduce a functor U : BA → Set that "forgets" the algebraic structure, mapping algebras and homomorphisms to their underlying sets and functions.

If we interpret the top arrow as a diagram in BA and the bottom triangle as a diagram in Set, then this diagram properly expresses that every function f : X → UB extends to a unique Boolean algebra homomorphism f′ : FX → B. The functor U can be thought of as a device to pull the homomorphism f′ back into Set so it can be related to f.

The remarkable aspect of this is that the latter diagram is one of the various (equivalent) definitions of when two functors are adjoint. Our F easily extends to a functor Set → BA, and our definition of X generating a free Boolean algebra FX is precisely that U has a left adjoint F.

Topological realization

The free Boolean algebra with κ generators, where κ is a finite or infinite cardinal number, may be realized as the collection of all clopen subsets of {0,1}^κ, given the product topology assuming that {0,1} has the discrete topology. For each α<κ, the αth generator is the set of all elements of {0,1}^κ whose αth coordinate is 1. In particular, the free Boolean algebra with generators is the collection of all clopen subsets of a Cantor space, sometimes called the Cantor algebra. Surprisingly, this collection is countable. In fact, while the free Boolean algebra with n generators, n finite, has cardinality 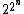, the free Boolean algebra with generators, as for any free algebra with generators and countably many finitary operations, has cardinality .

For more on this topological approach to free Boolean algebra, see Stone's representation theorem for Boolean algebras.

References

Steve Awodey (2006) Category Theory (Oxford Logic Guides 49). Oxford University Press.
Paul Halmos and Steven Givant (1998) Logic as Algebra. Mathematical Association of America.
Saunders Mac Lane (1998) Categories for the Working Mathematician. 2nd ed. (Graduate Texts in Mathematics 5). Springer-Verlag.
Saunders Mac Lane (1999) Algebra, 3d. ed. American Mathematical Society. {{ISBN|0-8218-1646-2}}.
Robert R. Stoll, 1963. Set Theory and Logic, chpt. 6.7. Dover reprint 1979.

2 : Boolean algebra|Free algebraic structures

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

A simple example

Category-theoretic definition

Topological realization

See also

References