“Friedlander–Iwaniec theorem”的意思、由来-开放百科全书

词条

Friedlander–Iwaniec theorem

释义

History
Special case
References
Further reading

In analytic number theory the Friedlander–Iwaniec theorem states that there are infinitely many prime numbers of the form 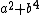. The first few such primes are

2, 5, 17, 37, 41, 97, 101, 137, 181, 197, 241, 257, 277, 281, 337, 401, 457, 577, 617, 641, 661, 677, 757, 769, 821, 857, 881, 977, … {{OEIS|id=A028916}}.

The difficulty in this statement lies in the very sparse nature of this sequence: the number of integers of the form 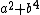less than is roughly of the order .

History

The theorem was proved in 1997 by John Friedlander and Henryk Iwaniec.^[1] Iwaniec was awarded the 2001 Ostrowski Prize in part for his contributions to this work.^[2]

Special case

When {{math|1=b = 1}}, the Friedlander–Iwaniec primes have the form 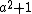, forming the set

2, 5, 17, 37, 101, 197, 257, 401, 577, 677, 1297, 1601, 2917, 3137, 4357, 5477, 7057, 8101, 8837, 12101, 13457, 14401, 15377, … {{OEIS|id=A002496}}.

It is conjectured (one of Landau's problems) that this set is infinite. However, this is not implied by the Friedlander–Iwaniec theorem.

References

1. ^{{Citation |last=Friedlander |first=John |last2=Iwaniec |first2=Henryk |year=1997 |title=Using a parity-sensitive sieve to count prime values of a polynomial |journal=PNAS |volume=94 |issue=4 |pages=1054–1058 |pmid=11038598|doi=10.1073/pnas.94.4.1054 |pmc=19742}}.
2. ^"Iwaniec, Sarnak, and Taylor Receive Ostrowski Prize"

History

Special case

References

Further reading