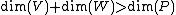“Fulton–Hansen connectedness theorem”的意思、由来-开放百科全书

词条

Fulton–Hansen connectedness theorem

释义

See also
References
External links

In mathematics, the Fulton–Hansen connectedness theorem is a result from intersection theory in algebraic geometry, for the case of subvarieties of projective space with codimension large enough to make the intersection have components of dimension at least 1. It is named after William Fulton and Johan Hansen, who proved it in 1979.

The formal statement is that if V and W are irreducible algebraic subvarieties of a projective space P, all over an algebraically closed field, and if

in terms of the dimension of an algebraic variety, then the intersection U of V and W is connected.

More generally, the theorem states that if is a projective variety and is any morphism such that , then 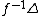is connected, where is the diagonal in . The special case of intersections is recovered by taking 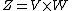, with the natural inclusion.

References

{{citation|first1=William|last1= Fulton|authorlink1=William Fulton (mathematician)|first2= Johan |last2=Hansen|title=A connectedness theorem for projective varieties with applications to intersections and singularities of mappings|journal= Annals of Mathematics |volume=110 |year=1979|pages= 159–166|doi=10.2307/1971249|jstor=1971249|issue=1|publisher=Annals of Mathematics}}
{{citation|first=Robert|last= Lazarsfeld|authorlink=Robert Lazarsfeld| title=Positivity in Algebraic Geometry|publisher= Springer|year= 2004}}

External links

PDF lectures with the result as Theorem 15.3 (attributed to Faltings, also)

2 : Intersection theory|Theorems in algebraic geometry

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

See also

References

External links