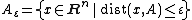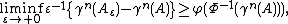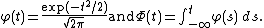- Mathematical formulation
- Remarks on the proofs
- See also
- References
In mathematics, the Gaussian isoperimetric inequality, proved by Boris Tsirelson and Vladimir Sudakov and independently by Christer Borell, states that among all sets of given Gaussian measure in the n-dimensional Euclidean space, half-spaces have the minimal Gaussian boundary measure.
Mathematical formulation
Let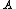 
be a measurable subset of 
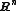endowed with the standard Gaussian measure 
with the density 
. Denote by
the ε-extension of A. Then the Gaussian isoperimetric inequality states that
where
Remarks on the proofs
The original proofs by Sudakov, Tsirelson and Borell were based on Paul Lévy's spherical isoperimetric inequality. Another approach is due to Bobkov, who introduced a functional inequality generalizing the Gaussian isoperimetric inequality and derived it from a certain two-point inequality. Bakry and Ledoux gave another proof of Bobkov's functional inequality based on the semigroup techniques which works in a much more abstract setting. Later Barthe and Maurey gave yet another proof using the Brownian motion.
The Gaussian isoperimetric inequality also follows from Ehrhard's inequality (cf. Latała, Borell).
See also
- Concentration of measure
- Borell–TIS inequality
References
- V.N.Sudakov, B.S.Cirelson [Tsirelson], Extremal properties of half-spaces for spherically invariant measures, (Russian) Problems in the theory of probability distributions, II, Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 41 (1974), 14–24, 165
- Ch. Borell, The Brunn-Minkowski inequality in Gauss space, Invent. Math. 30 (1975), no. 2, 207–216.
- S.G.Bobkov, An isoperimetric inequality on the discrete cube, and an elementary proof of the isoperimetric inequality in Gauss space, Ann. Probab. 25 (1997), no. 1, 206–214
- D.Bakry, M.Ledoux, Lévy-Gromov's isoperimetric inequality for an infinite-dimensional diffusion generator, Invent. Math. 123 (1996), no. 2, 259–281
- F. Barthe, B. Maurey, Some remarks on isoperimetry of Gaussian type, Ann. Inst. H. Poincaré Probab. Statist. 36 (2000), no. 4, 419–434.
- R. Latała, A note on the Ehrhard inequality, Studia Math. 118 (1996), no. 2, 169–174.
- Ch. Borell, The Ehrhard inequality, C. R. Math. Acad. Sci. Paris 337 (2003), no. 10, 663–666.
- Chamboret
- Chambornay-les-Bellevaux
- Chambornay-les-Pin
- Chambornay-lès-Bellevaux
- Chambornay-lès-Pin
- Chambors
- Chambost-Allieres
- Chambost-Allières
- Chambost-Longessaigne
- Chambouf
- Chambouf, Cote-d'Or
- Chambouf, Loire
- Chamboulive
- Chambourg-sur-Indre
- Chambray shirt
- Chambre Brabazon Ponsonby
- Chambrecy
- Chambre de bonne
- Chambre de commerce du Montréal métropolitain
- Chambre de commerce et d'industrie
- Chambre de Commerce et d'Industrie
- Chambre de commerce et d'industrie de Lyon
- Chambre Des Comptes
- Chambre des Comptes
- Chambre des comptes