“Generalized polygon”的意思、由来-开放百科全书

词条

Generalized polygon

释义

Definition
Examples
Restriction on parameters
Semi-finite generalized polygons
Combinatorial applications
See also
References

In mathematics, a generalized polygon is an incidence structure introduced by Jacques Tits in 1959. Generalized n-gons encompass as special cases projective planes (generalized triangles, n = 3) and generalized quadrangles (n = 4). Many generalized polygons arise from groups of Lie type, but there are also exotic ones that cannot be obtained in this way. Generalized polygons satisfying a technical condition known as the Moufang property have been completely classified by Tits and Weiss. Every generalized n-gon with n even is also a near polygon.

Definition

A generalized 2-gon (or a digon) is an incidence structure with at least 2 points and 2 lines where each point is incident to each line.

For a generalized n-gon is an incidence structure (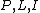), where is the set of points, is the set of lines and 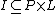is the incidence relation, such that:

It is a partial linear space.
It has no ordinary m-gons as subgeometry for .
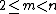It has an ordinary n-gon as a subgeometry.
For any 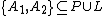there exists a subgeometry (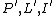) isomorphic to an ordinary n-gon such that .

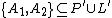An equivalent but sometimes simpler way to express these conditions is: consider the bipartite incidence graph with the vertex set 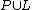and the edges connecting the incident pairs of points and lines.

The girth of the incidence graph is twice the diameter n of the incidence graph.

From this it should be clear that the incidence graphs of generalized polygons are Moore graphs.

A generalized polygon is of order (s,t) if:

all vertices of the incidence graph corresponding to the elements of have the same degree s + 1 for some natural number s; in other words, every line contains exactly s + 1 points,
all vertices of the incidence graph corresponding to the elements of have the same degree t + 1 for some natural number t; in other words, every point lies on exactly t + 1 lines.

We say a generalized polygon is thick if every point (line) is incident with at least three lines (points). All thick generalized polygons have an order.

The dual of a generalized n-gon (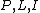), is the incidence structure with notion of points and lines reversed and the incidence relation taken to be the converse relation of . It can easily be shown that this is again a generalized n-gon.

Examples

The incidence graph of a generalized digon is a complete bipartite graph K_s+1,t+1.
For any natural n ≥ 3, consider the boundary of the ordinary polygon with n sides. Declare the vertices of the polygon to be the points and the sides to be the lines, with set inclusion as the incidence relation. This results in a generalized n-gon with s = t = 1.
For each group of Lie type G of rank 2 there is an associated generalized n-gon X with n equal to 3, 4, 6 or 8 such that G acts transitively on the set of flags of X. In the finite case, for n=6, one obtains the Split Cayley hexagon of order (q, q) for G₂(q) and the twisted triality hexagon of order (q³, q) for ³D₄(q³), and for n=8, one obtains the Ree-Tits octagon of order (q, q²) for ²F₄(q) with q = 2²ⁿ⁺¹. Up to duality, these are the only known thick finite generalized hexagons or octagons.

Restriction on parameters

Walter Feit and Graham Higman proved that finite generalized n-gons of order (s, t) with

s ≥ 2, t ≥ 2 can exist only for the following values of n:

2, 3, 4, 6 or 8.

Generalized "n"-gons for these values are referred to as generalized digons, triangles, quadrangles, hexagons and octagons.

When Feit-Higman theorem is combined with the Haemers-Roos inequalities, we get the following restrictions,

If n = 2, the incidence graph is a complete bipartite graph and thus "s", "t" can be arbitrary integers.
If n = 3, the structure is a finite projective plane, and s = t.
If n = 4, the structure is a finite generalized quadrangle, and t^1/2 ≤ s ≤ t².
If n = 6, then st is a square, and t^1/3 ≤ s ≤ t³.
If n = 8, then 2st is a square, and t^1/2 ≤ s ≤ t².
If s or t is allowed to be 1 and the structure is not the ordinary n-gon then besides the values of n already listed, only n = 12 may be possible.

Every known finite generalized hexagon of order (s, t) for s, t > 1 has order

(q, q): the split Cayley hexagons and their duals,
(q³, q): the twisted triality hexagon, or
(q, q³): the dual twisted triality hexagon,

where q is a prime power.

Every known finite generalized octagon of order (s, t) for s, t > 1 has order

(q, q²): the Ree-Tits octagon or
(q², q): the dual Ree-Tits octagon,

where q is an odd power of 2.

Semi-finite generalized polygons

If s and t are both infinite then generalized polygons exist for each n greater or equal to 2. It is unknown whether or not there exist generalized polygons with one of the parameters finite (and bigger than 1) while the other infinite (these cases are called semi-finite). Peter Cameron proved the non-existence of semi-finite generalized quadrangles with three points on each line, while Andries Brouwer and Bill Kantor independently proved the case of four points on each line. The non-existence result for five points on each line was proved by G. Cherlin using Model Theory.^[1] No such results are known without making any further assumptions for generalized hexagons or octagons, even for the smallest case of three points on each line.

Combinatorial applications

As noted before the incidence graphs of generalized polygons have important properties. For example, every generalized n-gon of order (s,s) is a (s+1,2n) cage. They are also related to expander graphs as they have nice expansion properties.^[2] Several classes of extremal expander graphs are obtained from generalized polygons.^[3] In Ramsey theory, graphs constructed using generalized polygons give us some of the best known constructive lower bounds on offdiagonal Ramsey numbers.^[4]

References

1. ^{{cite journal| doi=10.1016/j.disc.2004.04.021 | volume=291 | issue=1–3 | title=Locally finite generalized quadrangles with at most five points per line | year=2005 | journal=Discrete Mathematics | pages=73–79 | last1 = Cherlin | first1 = Gregory}}
2. ^{{Cite journal | doi=10.1137/0605030|title = Explicit Concentrators from Generalized N-Gons| journal=SIAM Journal on Algebraic and Discrete Methods| volume=5| issue=3| pages=287–293|year = 1984|last1 = Tanner|first1 = R. Michael}}
3. ^{{Cite arXiv |eprint = 1407.4562|last1 = Nozaki|first1 = Hiroshi|title = Linear programming bounds for regular graphs|class = math.CO|year = 2014}}
4. ^{{cite journal| doi=10.1016/j.jctb.2010.01.003 | volume=100 | issue=5 | title=Some constructive bounds on Ramsey numbers | year=2010 | journal=Journal of Combinatorial Theory, Series B | pages=439–445 | last1 = Kostochka | first1 = Alexandr | last2 = Pudlák | first2 = Pavel | last3 = Rödl | first3 = Vojtech}}

{{citation

| last1 = Godsil | first1 = Chris | author1-link = Chris Godsil
| last2 = Royle | first2 = Gordon | author2-link = Gordon Royle
| doi = 10.1007/978-1-4613-0163-9
| isbn = 978-0-387-95220-8
| location = New York
| mr = 1829620
| publisher = Springer-Verlag
| series = Graduate Texts in Mathematics
| title = Algebraic Graph Theory
| volume = 207
| year = 2001}}.

{{citation

| last1 = Feit | first1 = Walter | author1-link = Walter Feit
| last2 = Higman | first2 = Graham | author2-link = Graham Higman
| doi = 10.1016/0021-8693(64)90028-6
| journal = Journal of Algebra
| mr = 0170955
| pages = 114–131
| title = The nonexistence of certain generalized polygons
| volume = 1
| issue = 2 | year = 1964}}.

{{citation

| last1 = Haemers | first1 = W. H.
| last2 = Roos | first2 = C.
| doi = 10.1007/BF01447425
| journal = Geometriae Dedicata
| mr = 0170955
| pages = 219–222
| title = An inequality for generalized hexagons
| volume = 10
| issue = 1–4
| year = 1981}}.

{{cite book

| last = Kantor | first = W. M.
| title = Buildings and the Geometry of Diagrams
| chapter = Generalized polygons, SCABs and GABs
| series = Lecture Notes in Mathematics
| publisher = Springer-Verlag, Berlin
| volume = 1181
| pages = 79–158
| date = 1986
| doi = 10.1007/BFb0075513
| isbn = 978-3-540-16466-1
| citeseerx = 10.1.1.74.3986
}}

{{citation

| last = Van Maldeghem | first = Hendrik
| doi = 10.1007/978-3-0348-0271-0
| isbn = 978-3-7643-5864-8
| location = Basel
| mr = 1725957
| publisher = Birkhäuser Verlag
| series = Monographs in Mathematics
| title = Generalized polygons
| volume = 93
| year = 1998}}.

{{citation

| last = Stanton | first = Dennis
| doi = 10.1016/0097-3165(83)90036-5
| issue = 1
| journal = Journal of Combinatorial Theory
| mr = 685208
| pages = 15–27
| series = Series A
| title = Generalized n-gons and Chebychev polynomials
| volume = 34
| year = 1983}}.

{{citation

| last1 = Tits | first1 = Jacques | author1-link = Jacques Tits
| last2 = Weiss | first2 = Richard M.
| isbn = 978-3-540-43714-7
| location = Berlin
| mr = 1938841
| publisher = Springer-Verlag
| series = Springer Monographs in Mathematics
| title = Moufang polygons
| year = 2002}}.

2 : Group theory|Incidence geometry

随便看