“Generalized suffix tree”的意思、由来-开放百科全书

词条 Generalized suffix tree

释义

Functionality
Example
Alternatives
References
External links

In computer science, a generalized suffix tree is a suffix tree for a set of strings. Given the set of strings 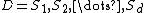of total length , it is a Patricia tree containing all suffixes of the strings. It is mostly used in bioinformatics.^[1]

Functionality

It can be built in time and space, and can be used to find all occurrences of a string of length in time, which is asymptotically optimal (assuming the size of the alphabet is constant^[2]{{rp|119}}).

When constructing such a tree, each string should be padded with a unique out-of-alphabet marker symbol (or string) to ensure no suffix is a substring of another, guaranteeing each suffix is represented by a unique leaf node.

Algorithms for constructing a GST include Ukkonen's algorithm (1995) and McCreight's algorithm (1976).

Example

A suffix tree for the strings ABAB and BABA is shown in a figure above. They are padded with the unique terminator strings $0 and $1. The numbers in the leaf nodes are string number and starting position. Notice how a left to right traversal of the leaf nodes corresponds to the sorted order of the suffixes. The terminators might be strings or unique single symbols. Edges on $ from the root are left out in this example.

Alternatives

An alternative to building a generalized suffix tree is to concatenate the strings, and build a regular suffix tree or suffix array for the resulting string. When hits are evaluated after a search, global positions are mapped into documents and local positions with some algorithm and/or data structure, such as a binary search in the starting/ending positions of the documents.

References

^[2]^[3]

External links

{{Commonscatinline}}
A C implementation of Generalized Suffix Tree for two strings

4 : Trees (data structures)|Substring indices|String data structures|Computer science suffixes

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。