“Gromov's inequality for complex projective space”的意思、由来-开放百科全书

词条

Gromov's inequality for complex projective space

释义

Projective planes over division algebras
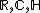
See also
References

In Riemannian geometry, Gromov's optimal stable 2-systolic inequality is the inequality

,

valid for an arbitrary Riemannian metric on the complex projective space, where the optimal bound is attained

by the symmetric Fubini–Study metric, providing a natural geometrisation of quantum mechanics. Here 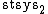is the stable 2-systole, which in this case can be defined as the infimum of the areas of rational 2-cycles representing the class of the complex projective line 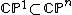in 2-dimensional homology.

The inequality first appeared in {{harvtxt|Gromov|1981}} as Theorem 4.36.

The proof of Gromov's inequality relies on the Wirtinger inequality for exterior 2-forms.

Projective planes over division algebras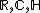

In the special case n=2, Gromov's inequality becomes 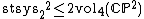. This inequality can be thought of as an analog of Pu's inequality for the real projective plane 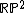. In both cases, the boundary case of equality is attained by the symmetric metric of the projective plane. Meanwhile, in the quaternionic case, the symmetric metric on 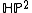is not its systolically optimal metric. In other words, the manifold 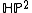admits Riemannian metrics with higher systolic ratio 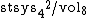than for its symmetric metric {{harv|Bangert|Katz|Shnider|Weinberger|2009}}.

References

{{cite journal | first1=Victor | last1=Bangert | first2=Mikhail G. | last2=Katz | first3=Steve | last3=Shnider | first4=Shmuel | last4=Weinberger | title=E₇, Wirtinger inequalities, Cayley 4-form, and homotopy| journal=Duke Mathematical Journal | volume=146 | year=2009 | issue=1 | pages=35–70 | arxiv=math.DG/0608006 | mr=2475399 | doi=10.1215/00127094-2008-061 | ref=harv}}
{{cite book | last=Gromov | first=Mikhail | title=Structures métriques pour les variétés riemanniennes | trans-title=Metric structures for Riemann manifolds | language=fr | editor1=J. Lafontaine | editor2=P. Pansu. | series=Textes Mathématiques | volume=1 | publisher=CEDIC | location=Paris | year=1981 | mr=0682063 | isbn=2-7124-0714-8 | ref=harv}}
{{cite book | last1=Katz | first1=Mikhail G. | title=Systolic geometry and topology|pages=19 | publisher=American Mathematical Society | location=Providence, R.I. | series=Mathematical Surveys and Monographs | isbn=978-0-8218-4177-8 | year=2007 | volume=137 | others=With an appendix by Jake P. Solomon. | mr=2292367 | doi=10.1090/surv/137}}

4 : Geometric inequalities|Differential geometry|Riemannian geometry|Systolic geometry

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Projective planes over division algebras

See also

References