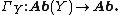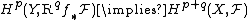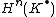- Examples The Leray spectral sequence Local-to-global Ext spectral sequence
- Derivation
- Notes
- References
In mathematics, in the field of homological algebra, the Grothendieck spectral sequence, introduced in Tôhoku paper, is a spectral sequence that computes the derived functors of the composition of two functors 
, from knowledge of the derived functors of F and G.
If 
and 
are two additive and left exact functors between abelian categories such that 
takes F-acyclic objects (e.g., injective objects) to 
-acyclic objects and if 
has enough injectives, then there is a spectral sequence for each object 
of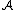 
that admits an F-acyclic resolution:
Many spectral sequences in algebraic geometry are instances of the Grothendieck spectral sequence, for example the Leray spectral sequence.
The exact sequence of low degrees reads
0 → R1G(FA) → R1(GF)(A) → G(R1F(A)) → R2G(FA) → R2(GF)(A).
Examples
The Leray spectral sequence
If 
and 
are topological spaces, let
and
be the category of sheaves of abelian groups on X and Y, respectively and
be the category of abelian groups.
For a continuous map
there is the (left-exact) direct image functor
.
We also have the global section functors
,
and
Then since
and the functors
and
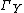
satisfy the hypotheses (since the direct image functor has an exact left adjoint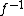 
, pushforwards of injectives are injective and in particular acyclic for the global section functor), the sequence in this case becomes:
for a sheaf 
of abelian groups on , and this is exactly the Leray spectral sequence.
Local-to-global Ext spectral sequence
There is a spectral sequence relating the global Ext and the sheaf Ext: let F, G be sheaves of modules over a ringed space 
; e.g., a scheme. Then
[1]
This is an instance of the Grothendieck spectral sequence: indeed,
,
and
.
Moreover, 
sends injective 
-modules to flasque sheaves,[2] which are 
-acyclic. Hence, the hypothesis is satisfied.
Derivation
We shall use the following lemma:
{{math_theorem|name=Lemma|If K is an injective complex in an abelian category C such that the kernels of the differentials are injective objects, then for each n,
is an injective object and for any left-exact additive functor G on C,
}}
Proof: Let 
be the kernel and the image of 
. We have
which splits.This implies each 
is injective. Next we look at
It splits, which implies the first part of the lemma, as well as the exactness of
Similarly we have (using the earlier splitting):
The second part now follows. 
We now construct a spectral sequence. Let 
be an F-acyclic resolution of A. Writing 
for 
, we have:
Take injective resolutions 
and 
of the first and the third nonzero terms. By the horseshoe lemma, their direct sum 
is an injective resolution of 
. Hence, we found an injective resolution of the complex:
such that each row 
satisfies the hypothesis of the lemma (cf. the Cartan–Eilenberg resolution.)
Now, the double complex 
gives rise to two spectral sequences, horizontal and vertical, which we are now going to examine. On the one hand, by definition,
,
which is always zero unless q = 0 since is G-acyclic by hypothesis. Hence, 
and 
. On the other hand, by the definition and the lemma,
Since 
is an injective resolution of 
(it is a resolution since its cohomology is trivial),
Since 
and 
have the same limiting term, the proof is complete.
Notes
2. ^{{harvnb|Godement|loc=Ch. II, Lemma 7.3.2.}}
References
- {{Citation | last1=Godement | first1=Roger | author1-link=Roger Godement | title=Topologie algébrique et théorie des faisceaux | publisher=Hermann | location=Paris |mr=0345092 | year=1973}}
- {{Weibel IHA}}