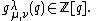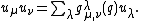“Hall algebra”的意思、由来-开放百科全书

词条

Hall algebra

释义

Construction
References

{{for|the more general Hall algebra of a category|Ringel–Hall algebra}}

In mathematics, the Hall algebra is an associative algebra with a basis corresponding to isomorphism classes of finite abelian p-groups. It was first discussed by {{harvtxt|Steinitz|1901}} but forgotten until it was rediscovered by {{harvs|txt|authorlink=Philip Hall|first= Philip|last= Hall|year=1959}}, both of whom published no more than brief summaries of their work. The Hall polynomials are the structure constants of the Hall algebra. The Hall algebra plays an important role in the theory of Masaki Kashiwara and George Lusztig regarding canonical bases in quantum groups. {{harvtxt|Ringel|1990}} generalized Hall algebras to more general categories, such as the category of representations of a quiver.

Construction

A finite abelian p-group M is a direct sum of cyclic p-power components 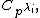where

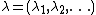is a partition of

called the type of M. Let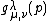

be the number of subgroups N of M such that N has type

and the quotient M/N has type

. Hall proved that the functions g are polynomial functions of p with integer coefficients. Thus we may replace p with an indeterminate q, which results in the Hall polynomials

Hall next constructs an associative ring over , now called the Hall algebra. This ring has a basis consisting of the symbols and the structure constants of the multiplication in this basis are given by the Hall polynomials:

It turns out that H is a commutative ring, freely generated by the elements 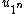corresponding to the elementary p-groups. The linear map from H to the algebra of symmetric functions defined on the generators by the formula

(where e_n is the nth elementary symmetric function) uniquely extends to a ring homomorphism and the images of the basis elements may be interpreted via the Hall–Littlewood symmetric functions. Specializing q to 0, these symmetric functions become Schur functions, which are thus closely connected with the theory of Hall polynomials.

References

{{citation|first=Philip|last=Hall|authorlink=Philip Hall|

year=1959|chapter=The algebra of partitions|title=Proceedings of the 4th Canadian mathematical congress, Banff|pages=147–159}}

George Lusztig, Quivers, perverse sheaves, and quantized enveloping algebras, Journal of the American Mathematical Society 4 (1991), no. 2, 365–421.
{{Citation | last1=Macdonald | first1=Ian G. | author1-link=Ian G. Macdonald | title=Symmetric functions and Hall polynomials | url=http://global.oup.com/academic/product/symmetric-functions-and-hall-polynomials-9780198504504 | publisher=The Clarendon Press Oxford University Press | edition=2nd | series=Oxford Mathematical Monographs | isbn=978-0-19-853489-1 | mr=1354144 | year=1995 }}
{{Citation | last1=Ringel | first1=Claus Michael | title=Hall algebras and quantum groups | doi=10.1007/BF01231516 | mr=1062796 | year=1990 | journal=Inventiones Mathematicae | volume=101 | issue=3 | pages=583–591| bibcode=1990InMat.101..583R }}
{{citation|contribution=Lectures on Hall algebras|last=Schiffmann|first=Olivier|title=Geometric methods in representation theory. II | pages=1–141|

series=Sémin. Congr.|volume= 24-II|publisher= Soc. Math. France| location=Paris|year= 2012|arxiv=math/0611617|mr=3202707 |bibcode=2006math.....11617S}}

{{citation|authorlink=Ernst Steinitz|last=Steinitz|first=Ernst|title=Zur Theorie der Abel'schen Gruppen|journal=Jahresbericht der Deutschen Mathematiker-Vereinigung|year=1901|volume=9|pages=80–85}}

3 : Algebras|Invariant theory|Symmetric functions

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。