无理数指数幂wulishu zhishumi

假设a是一个任意的正数，a是一个任意的正无理数，那么a^a叫做无理数指数幂.并规定：a^a是存在于以a为底，以a的不足近似值为指数与过剩近似值为指数的幂的数列之间，并等于这两个数列的共同的极限.
例如，设a= 10,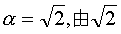的精确到0.1,0.01,0.001，…1/10ⁿ，…的不足近似值和过剩近似值，给出两个数列

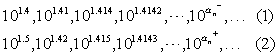
因为当底数大于1时，指数越大，这个幂的值也越大，所以数列(1)是递增数列，并且总小于10^1.5；同样数列(2)是递减数列，并且总大于10^1.4，即数列(1) (2)均是单调有界数列，故均有极限.因为

而

故

即

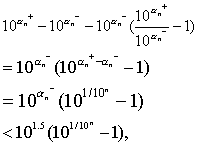
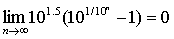
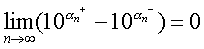
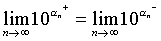
这就证明了数列(1)和(2)有共同的极限.这个极限是存在且唯一的.用
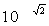
表示这个极限，即

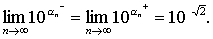
同时规定：a^-a＝1/aa(a> 0,a是正无理数).
零的正无理数次幂规定为零，零的负无理数次幂没有意义.例如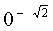无意义（零不能作除数）.
无理数指数幂的定义，在底数是负数时没有意义.例如，要确定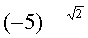的意义，需要用(-5)^1.4,(-5)^1.41，…来做它的近似值，但是分数指数幂在底数是负数时没有意义.
可以验证，有理指数幂的运算法则对于任意无理数指数幂仍能够适用.