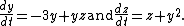- Main theorem
- Example
- See also
- References
- Further reading
- External links
In mathematics, in the study of dynamical systems, the Hartman–Grobman theorem or linearization theorem is a theorem about the local behavior of dynamical systems in the neighbourhood of a hyperbolic equilibrium point. It asserts that linearization—a natural simplification of the system—is effective in predicting qualitative patterns of behavior.
The theorem states that the behavior of a dynamical system in a domain near a hyperbolic equilibrium point is qualitatively the same as the behavior of its linearization near this equilibrium point, where hyperbolicity means that no eigenvalue of the linearization has real part equal to zero. Therefore, when dealing with such dynamical systems one can use the simpler linearization of the system to analyze its behavior around equilibria.[1]
Main theorem
Consider a system evolving in time with state 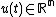 that satisfies the differential equation
that satisfies the differential equation  for some smooth map
for some smooth map  . Suppose the map has a hyperbolic equilibrium state
. Suppose the map has a hyperbolic equilibrium state 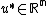 : that is,
: that is,  and the Jacobian matrix
and the Jacobian matrix 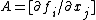 of
of  at state
at state  has no eigenvalue with real part equal to zero. Then there exists a neighborhood
has no eigenvalue with real part equal to zero. Then there exists a neighborhood  of the equilibrium
of the equilibrium  and a homeomorphism
and a homeomorphism 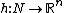 ,
,
such that  and such that in the neighbourhood
and such that in the neighbourhood  the flow of
the flow of  is topologically conjugate by the continuous map
is topologically conjugate by the continuous map  to the flow of its linearization
to the flow of its linearization 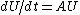 .[2][3][4][5]
.[2][3][4][5]
Even for infinitely differentiable maps  , the homeomorphism
, the homeomorphism  need not to be smooth, nor even locally Lipschitz. However, it turns out to be Hölder continuous, with an exponent depending on the constant of hyperbolicity of
need not to be smooth, nor even locally Lipschitz. However, it turns out to be Hölder continuous, with an exponent depending on the constant of hyperbolicity of  .[6]
.[6]
The Hartman–Grobman theorem has been extended to infinite-dimensional Banach spaces, non-autonomous systems  (potentially stochastic), and to cater for the topological differences that occur when there are eigenvalues with zero or near-zero real-part.[7][8][9][10]
(potentially stochastic), and to cater for the topological differences that occur when there are eigenvalues with zero or near-zero real-part.[7][8][9][10]
Example
The algebra necessary for this example is easily carried out by a web service that computes normal form coordinate transforms of systems of differential equations, autonomous or non-autonomous, deterministic or stochastic.[11]
Consider the 2D system in variables 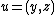 evolving according to the pair of coupled differential equations
evolving according to the pair of coupled differential equations
By direct computation it can be seen that the only equilibrium of this system lies at the origin, that is  . The coordinate transform,
. The coordinate transform, 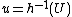 where
where 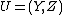 , given by
, given by
is a smooth map between the original 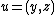 and new
and new 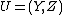 coordinates, at least near the equilibrium at the origin. In the new coordinates the dynamical system transforms to its linearisation
coordinates, at least near the equilibrium at the origin. In the new coordinates the dynamical system transforms to its linearisation
That is, a distorted version of the linearization gives the original dynamics in some finite neighbourhood.
See also
- Stable manifold theorem
References
2. ^{{cite journal|last = Grobman|first = D. M.|title=О гомеоморфизме систем дифференциальных уравнений|trans-title= Homeomorphisms of systems of differential equations|journal = Doklady Akademii Nauk SSSR|volume = 128|pages = 880–881|year = 1959}}
3. ^{{cite journal|last = Hartman|first = Philip|authorlink=Philip Hartman|title = A lemma in the theory of structural stability of differential equations|journal = Proc. A.M.S.|volume = 11|issue = 4|pages = 610–620|doi = 10.2307/2034720|date=August 1960|jstor=2034720}}
4. ^{{cite journal|last = Hartman|first = Philip|title = On local homeomorphisms of Euclidean spaces|journal = Bol. Soc. Math. Mexicana|volume = 5|pages = 220–241|year = 1960}}
5. ^{{cite book |first=C. |last=Chicone |title=Ordinary Differential Equations with Applications |volume=34 |series=Texts in Applied Mathematics |location= |publisher=Springer |edition=2nd |year=2006 |isbn=978-0-387-30769-5 }}
6. ^{{cite paper |first=Genrich |last=Belitskii |first2=Victoria |last2=Rayskin |year=2011 |title=On the Grobman–Hartman theorem in α-Hölder class for Banach spaces |work=Working paper |url=http://www.ma.utexas.edu/mp_arc/c/11/11-134.pdf }}
7. ^{{cite book |first=B. |last=Aulbach |first2=T. |last2=Wanner |chapter=Integral manifolds for Caratheodory type differential equations in Banach spaces |editor-first=B. |editor-last=Aulbach |editor2-first=F. |editor2-last=Colonius |title=Six Lectures on Dynamical Systems |pages=45–119 |publisher=World Scientific |location=Singapore |year=1996 |isbn=978-981-02-2548-3 }}
8. ^{{cite book |first=B. |last=Aulbach |first2=T. |last2=Wanner |chapter=Invariant Foliations for Carathéodory Type Differential Equations in Banach Spaces |editor-first=V. |editor-last=Lakshmikantham |editor2-first=A. A. |editor2-last=Martynyuk |title=Advances in Stability Theory at the End of the 20th Century |publisher=Gordon & Breach |year=1999 |isbn=978-0-415-26962-9 |citeseerx=10.1.1.45.5229 }}
9. ^{{cite journal | last1 = Aulbach | first1 = B. | last2 = Wanner | first2 = T. | year = 2000 | title = The Hartman–Grobman theorem for Caratheodory-type differential equations in Banach spaces | url = | journal = Non-linear Analysis | volume = 40 | issue = 1–8| pages = 91–104 | doi = 10.1016/S0362-546X(00)85006-3 }}
10. ^{{cite journal | last1 = Roberts | first1 = A. J. | year = 2008 | title = Normal form transforms separate slow and fast modes in stochastic dynamical systems | doi = 10.1016/j.physa.2007.08.023 | journal = Physica A | volume = 387 | issue = 1| pages = 12–38 | arxiv = math/0701623 | bibcode = 2008PhyA..387...12R }}
11. ^{{cite web |first=A. J. |last=Roberts |title=Normal form of stochastic or deterministic multiscale differential equations |url=http://www.maths.adelaide.edu.au/anthony.roberts/sdenf.php |year=2007 |archiveurl=https://web.archive.org/web/20131109164316/http://www.maths.adelaide.edu.au/anthony.roberts/sdenf.php |archivedate=November 9, 2013 }}
Further reading
- {{cite book |first=Lawrence |last=Perko |title=Differential Equations and Dynamical Systems |location=New York |publisher=Springer |edition=Third |year=2001 |isbn=978-0-387-95116-4 |pages=119–127 }}
External links
- {{cite journal|last = Coayla-Teran|first = E. |author2=Mohammed, S. |author3=Ruffino, P.|title = Hartman–Grobman Theorems along Hyperbolic Stationary Trajectories|journal = Discrete and Continuous Dynamical Systems|volume = 17|issue = 2|pages = 281–292|date=February 2007|url = http://sfde.math.siu.edu/Hartmangrobman.pdf|accessdate = 2007-03-09|doi = 10.3934/dcds.2007.17.281}}
- {{cite book| last = Teschl| given = Gerald|authorlink=Gerald Teschl| title = Ordinary Differential Equations and Dynamical Systems| publisher=American Mathematical Society| place = Providence| year = 2012| isbn= 978-0-8218-8328-0| url = http://www.mat.univie.ac.at/~gerald/ftp/book-ode/}}
- {{cite web |title=The Most Addictive Theorem in Applied Mathematics |url=https://blogs.scientificamerican.com/roots-of-unity/the-most-addictive-theorem-in-applied-mathematics/ |website=Scientific American}}