“Hereditarily countable set”的意思、由来-开放百科全书

词条

Hereditarily countable set

释义

See also
External links

In set theory, a set is called hereditarily countable if it is a countable set of hereditarily countable sets. This inductive definition is in fact well-founded and can be expressed in the language of first-order set theory. A set is hereditarily countable if and only if it is countable, and every element of its transitive closure is countable. If the axiom of countable choice holds, then a set is hereditarily countable if and only if its transitive closure is countable.

The class of all hereditarily countable sets can be proven to be a set from the axioms of Zermelo–Fraenkel set theory (ZF) without any form of the axiom of choice, and this set is designated 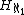. The hereditarily countable sets form a model of Kripke–Platek set theory with the axiom of infinity (KPI), if the axiom of countable choice is assumed in the metatheory.

If 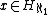, then .

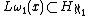More generally, a set is hereditarily of cardinality less than κ if and only if it is of cardinality less than κ, and all its elements are hereditarily of cardinality less than κ; the class of all such sets can also be proven to be a set from the axioms of ZF, and is designated . If the axiom of choice holds and the cardinal κ is regular, then a set is hereditarily of cardinality less than κ if and only if its transitive closure is of cardinality less than κ.

External links

[https://www.jstor.org/pss/2273380 "On Hereditarily Countable Sets"] by Thomas Jech

2 : Set theory|Large cardinals

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

See also

External links