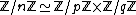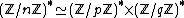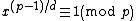“Higher residuosity problem”的意思、由来-开放百科全书

In cryptography, most public key cryptosystems are founded on problems that are believed to be intractable. The higher residuosity problem (also called the n th-residuosity problem^[1]) is one such problem. This problem is easier to solve than integer factorization, so the assumption that this problem is hard to solve is stronger than the assumption that integer factorization is hard.

Mathematical Background

If n is an integer, then the integers modulo n form a ring. If n=pq where p and q are primes, then the Chinese remainder theorem tells us that

The group of units of any ring form a group, and the group of units in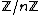

is traditionally denoted

as an isomorphism of groups. Since p and q were assumed to be prime, the groups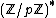

and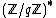

are cyclic of orders p-1 and q-1 respectively. If d is a divisor of p-1, then the set of dth powers in

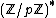form a subgroup of index d. If gcd(d,q-1) = 1, then every element in

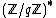is a dth power, so the set of dth powers in

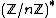is also a subgroup of index d. In general, if gcd(d,q-1) = g, then there are (q-1)/(g) dth powers in

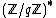, so the set of dth powers in

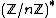has index dg.

This is most commonly seen when d=2, and we are considering the subgroup of quadratic residues, it is well known that exactly one quarter of the elements in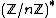

are

quadratic residues (when n is the product of exactly two primes, as it is here).

The important point is that for any divisor d of p-1 (or q-1) the set of dth powers forms a subgroup of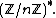

Problem Statement

Given an integer n = pq where p and q are unknown, an integer d such that d divides p-1, and an integer x < n, it is infeasible to determine whether x is a dth power (equivalently dth residue) modulo n.

Notice that if p and q are known it is easy to determine whether x is a dth residue modulo n because x will be a dth residue modulo p if and only if

Applications

The semantic security of the Benaloh cryptosystem and the Naccache-Stern cryptosystem rests on the intractability of this problem.

References

1. ^{{cite journal|last=Zhang|first=Yuliang|author2=Tsutomu Matsumoto |author3=Hideki Imai |title=Cryptographic Applications of th-Residuosity Problem with an Odd Integer|journal=Transactions of the IEICE|date=1988|volume=71|issue=8|pages=759-767|url=http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.137.8511|accessdate=14 February 2014}}