普遍二次曲面的主方向pubian erci qumian de zhu-fangxiang

若一个普遍二次曲面的径平面垂直于所平分的弦，则叫做主平面. 一个二次曲面至少有一个确定的主平面，最多有三个主平面，每两个主平面的交线叫做主轴. 一个二次曲面最多有三个主轴. 设普遍二次曲面的方程为： F (x,y,z) ≡ax²+ by²+ cz²+2fyz+2gzx+2hxy+2ux+2vy+2wz+d=0 (a²+b²+c²+f²+y²+h²≠0)，方程K³-K² (a+b+c) +K (A+B+C)—I³＝0，叫做F (x,y,z)=0的特征方程，它的根叫做特征根.式中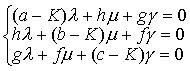A,B,C分别是I₃中a,b,c的代数余子式. 对于特征根K，以方程组：

所确定的一组λ:μ:γ作分量，所组成的向量，叫做该特征根所对应的特征向量，它的方向叫做主方向. 设K是一个特征根，且λ,μ,γ是它所对应的方向余弦，则K= (λ, μ, γ), 此处， (x, y, z) =ax²+by²+cz²+2fyz+2gzx+2hxy. 两个不相等的特征根所对应的主方向必垂直. 以三个主方向所建立的直角坐标系为新坐标系而作坐标轴的旋转，则 (x, y, z) =K₁x^′2+K₂y′ ²+K₃z^′2.