- Logical foundations
- References
- Further reading
- External links
Logical foundations
HOL Light is based on a formulation of type theory with equality
as the only primitive notion. The primitive rules of inference
are the following:
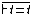 | REFL | reflexivity of equality |
 | TRANS | transitivity of equality |
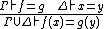 | MK_COMB | congruence of equality |
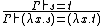 | ABS | abstraction of equality ( must not be free in must not be free in  ) ) |
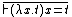 | BETA | connection of abstraction and function application |
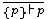 | ASSUME | assuming  , prove , prove  |
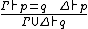 | EQ_MP | relation of equality and deduction |
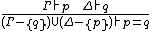 | DEDUCT_ANTISYM_RULE | deduce equality from 2-way deducibility |
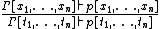 | INST | instantiate variables in assumptions and conclusion of theorem |
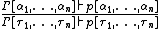 | INST_TYPE | instantiate type variables in assumptions and conclusion of theorem |
This formulation of type theory is very close to the one described in
section II.2 of {{Harvtxt|Lambek|Scott|1986}}.
References
1. ^https://github.com/jrh13/hol-light/
- {{Citation
| last1 = Lambek
| first1 = J
| authorlink1 = Joachim Lambek
| last2 = Scott
| first2 = P. J.
| title = Introduction to Higher Order Categorical logic
| publisher = Cambridge University Press
| year = 1986
| isbn = 9780521356534
}}
Further reading
- {{Citation
| author = Freek Wiedijk
| title = Formal Proof — Getting Started
| journal = Notices of the American Mathematical Society
|date=December 2008
| volume = 55
| issue = 11
| pages = 1408–1414
| url = http://www.ams.org/notices/200811/tx081101408p.pdf
| accessdate = 2008-12-14
}}
External links
- HOL Light
3 : Free theorem provers|Proof assistants|OCaml software
- 1st Guard Cavalry division (Russian Empire)
- 1st Guards Airborne Division
- 1st Guards Brigade
- 1st (Guards) Brigade
- 1st Guards Brigade (United Kingdom)
- 1st Guards Composite Aviation Division
- 1st Guards Division (Japan)
- 1st Guards Mechanized Corps
- 1st Guards Rifle Division
- 1st Guerrilla Regiment
- 1st Guided Missiles Squadron
- 1st Guldbagge Awards
- 1st (Halifax-Dartmouth) Field Artillery Regiment, RCA
- 1st Hampshire Engineers
- 1st Hampshire Engineer Volunteer Corps
- 1st Hampshire Royal Engineers (Volunteers)
- 1st Hand-Pelota doubles championship
- 1st Hand-Pelota singles championship
- 1st (Hanover Square) Middlesex Artillery Volunteer Corps
- 1st Health Support Battalion (Australia)
- 1st Heavy Artillery Regiment
- 1st (Heavy) Cavalry Brigade
- 1st Helpmann Awards
- 1st Highland Mounted Brigade
- 1st Hikō Sentai