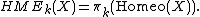“Homeotopy”的意思、由来-开放百科全书

词条

Homeotopy

释义

Definition
Example
References

In algebraic topology, an area of mathematics, a homeotopy group of a topological space is a homotopy group of the group of self-homeomorphisms of that space.

Definition

The homotopy group functors 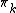assign to each path-connected topological space the group 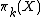of homotopy classes of continuous maps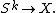

Another construction on a space is the group of all self-homeomorphisms , denoted 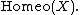If X is a locally compact, locally connected Hausdorff space then a fundamental result of R. Arens says that 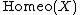will in fact be a topological group under the compact-open topology.

Under the above assumptions, the homeotopy groups for are defined to be:

Thus 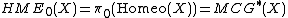is the extended mapping class group for 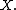In other words, the extended mapping class group is the set of connected components of 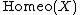as specified by the functor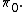

Example

According to the Dehn-Nielsen theorem, if is a closed surface then 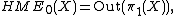the outer automorphism group of its fundamental group.

References

G.S. McCarty. Homeotopy groups. Trans. A.M.S. 106(1963)293-304.
R. Arens, Topologies for homeomorphism groups, Amer. J. Math. 68 (1946), 593–610.

2 : Algebraic topology|Homeomorphisms

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。