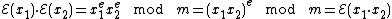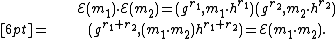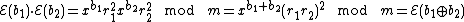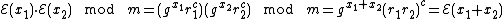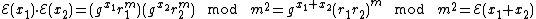1. Fully Homomorphic Encryption
    Homomorphic Cryptosystems In Current Use  Implementations  History of Homomorphic Cryptosystems  Gentry's cryptosystem  Cryptosystem over the integers 

2. Partially homomorphic cryptosystems
    Unpadded RSA  ElGamal  Goldwasser–Micali  Benaloh  Paillier  Other partially homomorphic cryptosystems 

3. Applications
    Encrypted database querying  Bitcoin split-key vanity mining 

4. See also

5. References

6. External links

Homomorphic encryption is a form of encryption that allows computation on ciphertexts, generating an encrypted result which, when decrypted, matches the result of the operations as if they had been performed on the plaintext.

Homomorphic encryption can be used for secure outsourced computation, for example secure cloud computing services, and securely chaining together different services without exposing sensitive data. For example, services from different companies can calculate 1) the tax, 2) the currency exchange rate, and 3) shipping on a transaction without exposing the unencrypted data to each of those services.^[1] Homomorphic encryption can also be used to create other secure systems such as secure voting systems,^[2] collision-resistant hash functions, private set intersection, and private information retrieval schemes. In typically highly regulated industries, such as health care, homomorphic encryption can be used to enable new services by removing privacy barriers inhibiting data sharing. For example, predictive analytics in health care can be hard to utilize due to medical data privacy concerns, but if the predictive analytics service provider can operate on encrypted data instead these privacy concerns are diminished.

Homomorphic encryption schemes are inherently malleable. In terms of malleability, homomorphic encryption schemes have weaker security properties than non-homomorphic schemes.

Fully Homomorphic Encryption

A cryptosystem that supports {{em|arbitrary computation}} on ciphertexts is known as fully homomorphic encryption (FHE). Such a scheme enables the construction of programs for any desirable functionality, which can be run on encrypted inputs to produce an encryption of the result. Since such a program need never decrypt its inputs, it can be run by an untrusted party without revealing its inputs and internal state.

Fully homomorphic cryptosystems have great practical implications in the outsourcing of private computations, for instance, in the context of cloud computing.^[3]

Homomorphic Cryptosystems In Current Use

Although there is a long history of homomorphic encryption research, the homomorphic cryptosystems in current use are derived from techniques that were developed starting in 2011-2012 by Zvika Brakerski, Craig Gentry, Vinod Vaikuntanathan, and others. These innovations led to the development of much more efficient somewhat and fully homomorphic cryptosystems. These include:

• The Brakerski-Gentry-Vaikuntanathan cryptosystem (BGV),^[4] building on techniques of Brakerski-Vaikuntanathan.^[5]
• Brakerski's {{em|scale-invariant}} cryptosystem.^[6]
• The NTRU-based cryptosystem due to Lopez-Alt, Tromer, and Vaikuntanathan (LTV).^[7]
• The Gentry-Sahai-Waters cryptosystem (GSW).^[8]
• The Brakerski/Fan-Vercauteren cryptosystem (BFV).^[9]
• The Cheon-Kim-Kim-Song cryptosystem (CKKS).^[10]

The security of most of these schemes is based on the hardness of the Learning with errors problem, except for the LTV scheme whose security is based on a variant of the NTRU computational problem, and the FV scheme which is based on the Ring Learning with errors variant of this problem. The distinguishing characteristic of these cryptosystems is that they all feature much slower growth of the noise during the homomorphic computations.

Additional optimizations by Craig Gentry, Shai Halevi, and Nigel Smart resulted in cryptosystems with nearly optimal asymptotic complexity: Performing 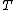operations on data encrypted with security parameter has complexity of only 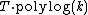.^[11][12][13]

These optimizations build on the Smart-Vercauteren techniques that enables packing of many plaintext values in a single ciphertext and operating on all these plaintext values in a SIMD fashion.^[14]

Many of the advances in these second-generation cryptosystems were also ported to the cryptosystem over the integers.^[15][16]

This type of circuits, however, seems incompatible with the ciphertext-packing techniques, and hence the Gentry-Halevi-Smart optimizations^[11] cannot be applied here.

All the second-generation cryptosystems still follow the basic blueprint of Gentry's original construction, namely they first construct a somewhat-homomorphic cryptosystem that handles noisy ciphertexts, and then convert it to a fully homomorphic cryptosystem using bootstrapping.

Implementations

There are several implementation of current fully homomorphic encryption available in open source libraries:

• HElib^[16] by Shai Halevi and Victor Shoup that implements the BGV cryptosystem with the GHS optimizations;
• PALISADE^[17] by a consortium of defense contractors and academics funded by DARPA, IARPA, NIH and Sloan Foundation, including New Jersey Institute of Technology, Duality Technologies, Raytheon BBN Technologies, MIT, University of California, San Diego and others. PALISADE is a framework for implementing lattice cryptography primitives and comes with implementations of multiple fully homomorphic encryption schemes including the BFV^[9] and BGV cryptosystems;
• HEAAN^[18] by Seoul National University, the original homomorphic encryption library that implements CKKS^[10] cryptosystem including a bootstrapping algorithm^[19];
• Microsoft SEAL^[20] by Microsoft implements the BFV^[9] and the CKKS^[10] encryption schemes;
• FHEW^[21] by Leo Ducas and Daniele Micciancio that implements a combination of Regev's LWE cryptosystem with the bootstrapping techniques of Alperin-Sheriff and Peikert,^[15];
• TFHE^[22] by Ilaria Chillotti, Nicolas Gama, Mariya Georgieva and Malika Izabachene that proposes a faster variant over the Torus with an intuitive API to evaluate boolean circuits.

Some of these libraries implement bootstrapping: HElib reports a time of 5–10 minutes for bootstrapping a packed ciphertext with about 1000 plaintext values,^[23]

FHEW reports a time of around {{Half}} second for bootstrapping a non-packed ciphertext encrypting a single bit,^[24]

TFHE reports a time of 13 milliseconds for evaluating any bootstrapped binary gate on non-packed ciphertexts encrypting a single bit,^[25]

and HEAAN reports a time of 2 minutes for bootstrapping a packed ciphertext with 128 plaintext values of 12-bit precision.^[19]

In late 2014, a re-implementation of homomorphic evaluation of the AES-encryption circuit using HElib reported an evaluation time of just over 4 minutes on 120 inputs, bringing the amortized per-input time to about 2 seconds.^[16]

A standardization effort for homomorphic encryption maintains another list of implementations.

History of Homomorphic Cryptosystems

The problem of constructing a fully homomorphic encryption scheme was first proposed in 1978, within a year of the development of RSA.^[26] For more than 30 years, it was unclear whether a solution existed. During that period, partial results included the Sander-Young-Yung system, which after more than 20 years solved the problem for logarithmic depth circuits;^[27] the Boneh–Goh–Nissim cryptosystem, which supports evaluation of an unlimited number of addition operations but at most one multiplication;^[28]

and the Ishai-Paskin cryptosystem, which supports evaluation of polynomial-size branching programs.^[29]

Gentry's cryptosystem

Craig Gentry,^[30] using lattice-based cryptography, described the first plausible construction for a fully homomorphic encryption scheme. Gentry's scheme supports both addition and multiplication operations on ciphertexts, from which it is possible to construct circuits for performing arbitrary computation.

The construction starts from a somewhat homomorphic encryption scheme, which is limited to evaluating low-degree polynomials over encrypted data. (It is limited because each ciphertext is noisy in some sense, and this noise grows as one adds and multiplies ciphertexts, until ultimately the noise makes the resulting ciphertext indecipherable.) Gentry then shows how to slightly modify this scheme to make it bootstrappable, i.e., capable of evaluating its own decryption circuit and then at least one more operation. Finally, he shows that any bootstrappable somewhat homomorphic encryption scheme can be converted into a fully homomorphic encryption through a recursive self-embedding.

For Gentry's "noisy" scheme, the bootstrapping procedure effectively "refreshes" the ciphertext by applying to it the decryption procedure homomorphically, thereby obtaining a new ciphertext that encrypts the same value as before but has lower noise. By "refreshing" the ciphertext periodically whenever the noise grows too large, it is possible to compute arbitrary number of additions and multiplications without increasing the noise too much.

Gentry based the security of his scheme on the assumed hardness of two problems: certain worst-case problems over ideal lattices, and the sparse (or low-weight) subset sum problem.

Gentry's Ph.D. thesis^[31]

provides additional details.

Regarding performance, ciphertexts in Gentry's scheme remain compact insofar as their lengths do not depend at all on the complexity of the function that is evaluated over the encrypted data, but the scheme is impractical, and its ciphertext size and computation time increase sharply as one increases the security level.

Several optimizations and refinements were proposed by Damien Stehle and Ron Steinfeld,^[32]

and Craig Gentry and Shai Halevi,^[35][36]

the latter obtaining the first working implementation of Gentry's fully homomorphic encryption.

There have been several early implementations of fully homomorphic encryption capabilities. The Gentry-Halevi implementation of the above mentioned Gentry's original cryptosystem;^[36] reported timing of about 30 minutes per basic bit operation. Extensive design and implementation work in subsequent years have improved upon these early implementations by many orders of magnitude runtime performance.

An early implementation from 2012 due to Gentry, Halevi, and Smart (GHS)^[13] of a variant of the BGV cryptosystem,^[4] reported evaluation of a complex circuit (implementing the encryption procedure of the AES cipher) in 36 hours. Using the packed-ciphertext techniques, that implementation could evaluate the same circuit on 54 different inputs in the same 36 hours, yielding amortized time of roughly 40 minutes per input. This AES-encryption circuit was adopted as a benchmark in several follow-up works,^[15][37][38] gradually bringing the evaluation time down to about four hours and the per-input amortized time to just over 7 seconds.

Cryptosystem over the integers

In 2010, Marten van Dijk, Craig Gentry, Shai Halevi and Vinod Vaikuntanathan presented a second fully homomorphic encryption scheme,^[39]

which uses many of the tools of Gentry's construction, but which does not require ideal lattices. Instead, they show that the somewhat homomorphic component of Gentry's ideal lattice-based scheme can be replaced with a very simple somewhat homomorphic scheme that uses integers. The scheme is therefore conceptually simpler than Gentry's ideal lattice scheme, but has similar properties with regards to homomorphic operations and efficiency. The somewhat homomorphic component in the work of van Dijk et al. is similar to an encryption scheme proposed by Levieil and Naccache in 2008,^[40] and also to one that was proposed by Bram Cohen in 1998.^[41]

Cohen's method is not even additively homomorphic, however. The Levieil–Naccache scheme supports only additions, but it can be modified to also support a small number of multiplications.

Many refinements and optimizations of the scheme of van Dijk et al. were proposed in a sequence of works by Jean-Sébastien Coron, Tancrède Lepoint, Avradip Mandal, David Naccache, and Mehdi Tibouchi.^{[42][43][44][45]}

Some of these works included also implementations of the resulting schemes.

Partially homomorphic cryptosystems

In the following examples, the notation 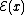is used to denote the encryption of the message .

Unpadded RSA

If the RSA public key is modulus and exponent , then the encryption of a message is given by 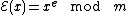. The homomorphic property is then

ElGamal

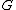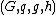In the ElGamal cryptosystem, in a cyclic group of order with generator , if the public key is , where 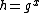, and is the secret key, then the encryption of a message is 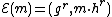, for some random 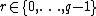. The homomorphic property is then

Goldwasser–Micali

In the Goldwasser–Micali cryptosystem, if the public key is the modulus m and quadratic non-residue x, then the encryption of a bit b is 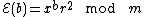, for some random . The homomorphic property is then

where denotes addition modulo 2, (i.e. exclusive-or).

Benaloh

In the Benaloh cryptosystem, if the public key is the modulus m and the base g with a blocksize of c, then the encryption of a message x is 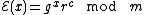, for some random . The homomorphic property is then

Paillier

In the Paillier cryptosystem, if the public key is the modulus m and the base g, then the encryption of a message x is 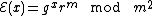, for some random . The homomorphic property is then

Other partially homomorphic cryptosystems

• Okamoto–Uchiyama cryptosystem
• Naccache–Stern cryptosystem
• Damgård–Jurik cryptosystem
• Sander-Young-Yung encryption scheme
• Boneh–Goh–Nissim cryptosystem
• Ishai-Paskin cryptosystem

Applications

Encrypted database querying

Typical database encryption leaves the database encrypted at rest, but when queries are performed the data must be decrypted in order to be parsed. Homomorphic encryption schemes have been devised such that database queries can run against ciphertext data directly.^[46] It must be noted that in this paper, the authors have accepted that they have used simple and non secure homomorphic scheme and still it takes a huge toll on the performance. For e.g. a 16 bit multiplication takes approximately 24 minutes.

Bitcoin split-key vanity mining

Bitcoin addresses are hashes of public keys from ECDSA key pairs. A vanity address is an address generated from parameters such that the resultant hash contains a human-readable string (e.g., 1BoatSLRHtKNngkdXEeobR76b53LETtpyT). Given that ECDSA key pairs have homomorphic properties for addition and multiplication, one can outsource the generation of a vanity address without having the generator know the full private key for this address.

For example,

1. Alice generates a private key (a) and public key (A) pair, and publicly posts A.
2. Bob generates a key pair (b, B) such that hash(A + B) results in a desired vanity address. He sells b and B to Alice. A, B, and b are publicly known, so one can verify that the address = hash(A + B) is desired.
3. Alice computes the combined private key (a + b) and uses it as the private key for the public key (A + B).

Similarly, multiplication could be used instead of addition.

See also

• Homomorphic secret sharing
• Homomorphic signatures for network coding
• Private biometrics
• Verifiable computing using a fully homomorphic scheme
• Client-side encryption
• Secure multi-party computation
• Format-preserving encryption

References

External links

• HomomorphicEncryption.org; an open standardization effort for fully homomorphic encryption
• The Swiss Army Knife of Cryptography
• {{Cite news|url=https://www.americanscientist.org/article/alice-and-bob-in-cipherspace|title=Alice and Bob in Cipherspace|date=September 2012|work=American Scientist|access-date=2018-05-08|language=en}}
• [https://github.com/hcrypt-project/libScarab The Open Source hcrypt Project]
• [https://github.com/shaih/HElib HElib], open source homomorphic encryption library for C++
• [https://github.com/lducas/FHEW FHEW], open source homomorphic encryption library for C and C++
• [https://git.njit.edu/palisade/PALISADE PALISADE], open source lattice cryptography framework; written in C++
• [https://www.microsoft.com/en-us/research/project/microsoft-seal Microsoft SEAL], open source homomorphic encryption library by Microsoft; written in C++
• [https://tfhe.github.io/tfhe TFHE], open source homomorphic encryption library for C and C++

• Ammunition Hill
• Ammunition hoist
• Ammunition Identification Code
• Ammunition magazines
• Ammunition store
• Ammurin
• `Ammuriya
• `Ammuriya (disambiguation)
• Ammuriya, Nablus
• Ammutseba
• Ammuvinde Aattinkutti
• Ammuvinte Aangalamar
• Ammuvinte Aattinkutty
• AMM v HXW
• Ammy Virk
• Ammyy
• AMMYY scam
• Ammæli
• AMM – Association for Machines and Mechanisms
• AM&N
• Amna Bakheet
• Amna Ilyas
• Amna Inayat Medical College
• Amnaj Ruenroeng
• Amnart Chalermchaowarit