“Ho–Lee model”的意思、由来-开放百科全书

词条

Ho–Lee model

释义

References
External links

In financial mathematics, the Ho–Lee model is a short rate model widely used in the pricing of bond options, swaptions and other interest rate derivatives, and in modeling future interest rates.^[1]{{rp|381}} It was developed in 1986 by Thomas Ho and Sang Bin Lee.

Under this model, the short rate follows a normal process:

The model can be calibrated to market data by implying the form of 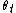from market prices, meaning that it can exactly return the price of bonds comprising the yield curve. This calibration, and subsequent valuation of bond options, swaptions and other interest rate derivatives, is typically performed via a binomial lattice based model. Closed form valuations of bonds, and "Black-like" bond option formulae are also available.^[1]

As the model generates a symmetric ("bell shaped") distribution of rates in the future, negative rates are possible. Further, it does not incorporate mean reversion. For both of these reasons, models such as Black–Derman–Toy (lognormal and mean reverting) and Hull–White (mean reverting with lognormal variant available) are often preferred.^[2]{{rp|385}} The Kalotay–Williams–Fabozzi model is a lognormal analogue to the Ho–Lee model, although is less widely used than the latter two.

References

Notes

1. ^Graeme West, (2010). Interest Rate Derivatives, Financial Modelling Agency.
2. ^¹Pietro Veronesi (2010). Fixed Income Securities: Valuation, Risk, and Risk Management. Wiley. {{ISBN|0-470-10910-6}}

Primary references

T.S.Y. Ho, S.B. Lee, Term structure movements and pricing interest rate contingent claims, Journal of Finance 41, 1986. {{doi|10.2307/2328161}}
John C. Hull, Options, futures, and other derivatives, 5th edition, Prentice Hall, {{ISBN|0-13-009056-5}}

External links

Valuation and Hedging of Interest Rates Derivatives with the Ho-Lee Model, Markus Leippold and Zvi Wiener, Wharton School
Term Structure Lattice Models, Martin Haugh, Columbia University

Online tools

Binomial Tree – Excel implementation, thomasho.com

3 : Fixed income analysis|Short-rate models|Financial models

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。