1. References

  name       =hyperbolic|  type       =density|  pdf_image  =|  cdf_image  =|  parameters = location (real)
  (real)
 asymmetry parameter (real)
 scale parameter (real)
|  support    =|  pdf        = 

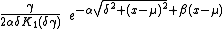
 denotes a modified Bessel function of the second kind|  cdf        =|  mean       =|  median     =|  mode       =|  variance   =|  skewness   =|  kurtosis   =|  entropy    =|  mgf        =|  char       =|

The hyperbolic distribution is a continuous probability distribution characterized by the logarithm of the probability density function being a hyperbola. Thus the distribution decreases exponentially, which is more slowly than the normal distribution. It is therefore suitable to model phenomena where numerically large values are more probable than is the case for the normal distribution. Examples are returns from financial assets and turbulent wind speeds. The hyperbolic distributions form a subclass of the generalised hyperbolic distributions.

The origin of the distribution is the observation by Ralph Alger Bagnold, published in his book The Physics of Blown Sand and Desert Dunes (1941), that the logarithm of the histogram of the empirical size distribution of sand deposits tends to form a hyperbola. This observation was formalised mathematically by Ole Barndorff-Nielsen in a paper in 1977,^[1] where he also introduced the generalised hyperbolic distribution, using the fact the a hyperbolic distribution is a random mixture of normal distributions.

References

• Pīdòu dàhuì
• Pīlu
• Pī Lín pī Kǒng yùndòng
• Pīnyīn
• Pīnyīn (disambiguation)
• Pīr Panjāl
• Pīr Panjāl Range
• Pīshīn
• Pınar
• Pınarbaşı (disambiguation)
• Pınar Köksal
• Pınarlı
• Pınar İlkkaracan
• Pırlanta - Tek Taşımı Kendim Aldım
• Pļaviņas Hydroelectric Power Station
• Pļaviņas Hydro Power Plant
• Pļaviņas Municipality
• Pļaviņas Station
• Pļaviņas–Gulbene Railway
• Pļaviņu HES
• Pļaviņu novads
• Pļaviŋās
• Płachty
• Płachty, Masovian Voivodeship
• Płachty, Pomeranian Voivodeship