- Definitions
- History
- Bucket handle example
- Properties
- In dynamical systems
- See also
- References
- External links
In point-set topology, an indecomposable continuum is a continuum that is indecomposable, i.e. that cannot be expressed as the union of any two of its proper subcontinua. In 1910, L. E. J. Brouwer was the first to describe an indecomposable continuum.
Indecomposable continua have been used by topologists as a source of counterexamples. They also occur in dynamical systems.
Definitions
A continuum  is a nonempty compact connected metric space. The arc, the n-sphere, and the Hilbert cube are examples of path connected continua; the topologist's sine curve and Warsaw circle are examples of non-path connected continua. A subcontinuum
is a nonempty compact connected metric space. The arc, the n-sphere, and the Hilbert cube are examples of path connected continua; the topologist's sine curve and Warsaw circle are examples of non-path connected continua. A subcontinuum  of a continuum
of a continuum  is a closed, connected subset of
is a closed, connected subset of  . A space is nondegenerate if it is not equal to a single point. A continuum
. A space is nondegenerate if it is not equal to a single point. A continuum  is decomposable if there exist two subcontinua
is decomposable if there exist two subcontinua  and
and  of
of  such that
such that 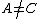 and
and 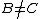 but
but 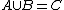 . A continuum which is not decomposable is an indecomposable continuum. A continuum
. A continuum which is not decomposable is an indecomposable continuum. A continuum  in which every subcontinuum is indecomposable is said to be hereditarily indecomposable. A composant of an indecomposable continuum
in which every subcontinuum is indecomposable is said to be hereditarily indecomposable. A composant of an indecomposable continuum  is a maximal set in which any two points lie within some proper subcontinuum of
is a maximal set in which any two points lie within some proper subcontinuum of  . A continuum
. A continuum  is irreducible between
is irreducible between  and
and 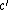 if
if  and no proper subcontinuum contains both points. An indecomposable continuum is irreducible between any two of its points.[1]
and no proper subcontinuum contains both points. An indecomposable continuum is irreducible between any two of its points.[1]
History
Bucket handle example
Indecomposable continua are often constructed as the limit of a sequence of nested intersections, or (more generally) as the inverse limit of a sequence of continua. The buckethandle, or Brouwer–Janiszewski–Knaster continuum, is often used the simplest example of an indecomposable continuum, and can be so constructed (see upper right). Alternatively, take the Cantor ternary set  projected onto the interval
projected onto the interval  of the
of the  -axis in the plane. Let
-axis in the plane. Let 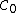 be the family of semicircles above the
be the family of semicircles above the  -axis with center
-axis with center 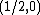 and with endpoints on
and with endpoints on  (which is symmetric about this point). Let
(which is symmetric about this point). Let 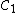 be the family of semicircles below the
be the family of semicircles below the  -axis with center the midpoint of the interval
-axis with center the midpoint of the interval 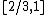 and with endpoints in
and with endpoints in 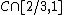 . Let
. Let  be the family of semicircles below the
be the family of semicircles below the  -axis with center the midpoint of the interval
-axis with center the midpoint of the interval 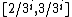 and with endpoints in
and with endpoints in 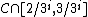 . Then the union of all such
. Then the union of all such  is the bucket handle.[4]
is the bucket handle.[4]
The bucket handle admits no Borel transversal, that is there is no Borel set containing exactly one point from each composant.
Properties
In a sense, 'most' continua are indecomposable. Let  be an
be an  -cell with metric
-cell with metric  ,
, 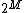 the set of all nonempty closed subsets of
the set of all nonempty closed subsets of  , and
, and 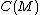 the hyperspace of all connected members of
the hyperspace of all connected members of 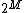 equipped with the Hausdorff metric
equipped with the Hausdorff metric  defined by
defined by 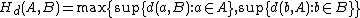 . Then the set of nondegenerate indecomposable subcontinua of
. Then the set of nondegenerate indecomposable subcontinua of  is dense in
is dense in 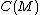 .
.
In dynamical systems
In 1932 George Birkhoff described his "remarkable closed curve", a homeomorphism of the annulus that contained an invariant continuum. Marie Charpentier showed that this continuum was indecomposable, the first link from indecomposable continua to dynamical systems. The invariant set of a certain Smale horseshoe map is the bucket handle. Marcy Barge and others have extensively studied indecomposable continua in dynamical systems.[5]
See also
- Indecomposability
- Lakes of Wada, three open subsets of the plane whose boundary is an indecomposable continuum
- Solenoid
- Sierpinski carpet
References
2. ^{{citation|journal=Mathematische Annalen|year=1910|volume= 68|issue =3|pages=422–434|title=Zur Analysis Situs|first=L. E. J.|last= Brouwer|doi=10.1007/BF01475781}}
3. ^{{cite book|last1=Cook|first1=Howard|last2=Ingram|first2=William T.|last3=Kuperberg|first3=Krystyna|last4=Lelek|first4=Andrew|last5=Minc|first5=Piotr|title=Continua: With the Houston Problem Book|date=1995|publisher=CRC Press|isbn=9780824796501|pages=103|url=https://books.google.com/books?id=bVcZGMOA4AEC&pg=PA103|language=en}}
4. ^{{cite book|last1=Ingram|first1=W. T.|last2=Mahavier|first2=William S.|title=Inverse Limits: From Continua to Chaos|date=2011|publisher=Springer Science & Business Media|isbn=9781461417972|pages=16|url=https://books.google.com/books?id=II3W2CZxDYMC&pg=PA16|language=en}}
5. ^{{cite journal|last1=Kennedy|first1=Judy|title=How Indecomposable Continua Arise in Dynamical Systems|journal=Annals of the New York Academy of Sciences|date=1 December 1993|volume=704|issue=1|pages=180–201|doi=10.1111/j.1749-6632.1993.tb52522.x|language=en|issn=1749-6632}}
External links
- {{cite book | first=S. | last=Solecki | chapter=Descriptive set theory in topology | pages=506–508 | title=Recent progress in general topology II | editor1-last=Hušek | editor1-first=M. | editor2-last=van Mill | editor2-first=J. | publisher=Elsevier | year=2002 | isbn=978-0-444-50980-2 }}
- {{citation|journal=Notices of the AMS|url=http://www.ams.org/notices/201406/201406-about-the-cover.pdf|year=2014|volume=61|title=About the cover|last=Casselman|first=Bill|pages=610, 676}} explains Brouwer's picture of his indecomposable continuum that appears on the front cover of the journal.
- Gare d'Albi-Ville
- Gare d'Alencon
- Gare d'Alençon
- Gare d'Alet-les-Bains
- Gare d'Allassac
- Gare d'Amboise
- Gare d'Amiens Saint-Roch
- Gare d'Andorre-L'Hospitalet
- Gare d'Angers
- Gare d'Angers-Saint-Laud
- Gare d'Angers Saint-Laud
- Gare d'Angerville
- Gare d'Angouleme
- Gare d'Angoulême
- Gare d'Annecy
- Gare d'Argentan
- Gare d'Arles
- Gare d'Arras
- Gare d'Artenay
- Gare d'Artix
- Gare d'Ascq
- Gare d'Asnieres-sur-Seine
- Gare d'Assat
- Gare d'Assier
- Gare d'Aubagne