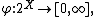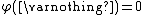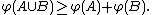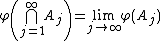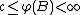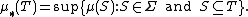“Inner measure”的意思、由来-开放百科全书

词条

Inner measure

释义

Definition
The inner measure induced by a measure
Measure completion
References

In mathematics, in particular in measure theory, an inner measure is a function on the set of all subsets of a given set, with values in the extended real numbers, satisfying some technical conditions. Intuitively, the inner measure of a set is a lower bound of the size of that set.

Definition

An inner measure is a function

defined on all subsets of a set X, that satisfies the following conditions:

Null empty set: The empty set has zero inner measure (see also: measure zero).

Superadditive: For any disjoint sets A and B,

Limits of decreasing towers: For any sequence {A_j} of sets such that 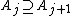for each j and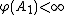

Infinity must be approached: If 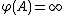for a set A then for every positive number c, there exists a B which is a subset of A such that,

The inner measure induced by a measure

Let Σ be a σ-algebra over a set X and μ be a measure on Σ.

Then the inner measure μ_* induced by μ is defined by

Essentially μ_* gives a lower bound of the size of any set by ensuring it is at least as big as the μ-measure of any of its Σ-measurable subsets. Even though the set function μ_* is usually not a measure, μ_* shares the following properties with measures:

μ_*(∅)=0,
μ_* is non-negative,
If E ⊆ F then μ_*(E) ≤ μ_*(F).

Measure completion

Induced inner measures are often used in combination with outer measures to extend a measure to a larger σ-algebra. If μ is a finite measure defined on a σ-algebra Σ over X and μ^* and μ_* are corresponding induced outer and inner measures, then the sets T ∈ 2^X such that μ_*(T) = μ^*(T) form a σ-algebra 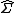with 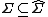.^[1] The set function μ̂ defined by

,

for all 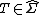is a measure on 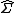known as the completion of μ.

References

1. ^Halmos 1950, § 14, Theorem F

Halmos, Paul R., Measure Theory, D. Van Nostrand Company, Inc., 1950, pp. 58.
A. N. Kolmogorov & S. V. Fomin, translated by Richard A. Silverman, Introductory Real Analysis, Dover Publications, New York, 1970, {{ISBN|0-486-61226-0}} (Chapter 7)

1 : Measures (measure theory)

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。