极值jizhi

设函数y=f(x)在点x₀的邻域内有定义，若存在x₀的某邻域(x₀-δ,x₀+δ)，在此邻域内恒有f(x₀)≥f(x)(f(x0)≤f(x))则称f(x₀)为f(x)的一个极大值（极小值），点x0称为极大值点（极小值点）.极大值与极小值统称为极值，极大值点与极小值点统称为极值点.

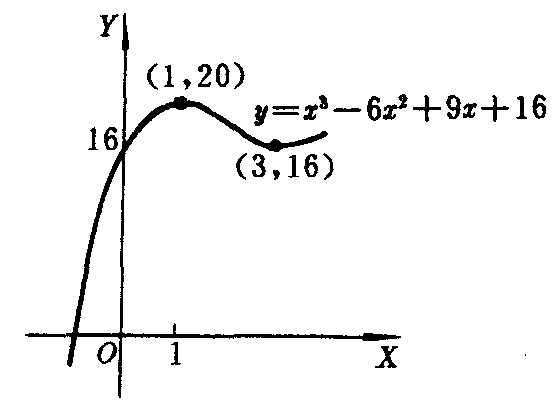
图1

例如，函数f(x)=x³-6x²+9x+16，在(-∞,1)内是单调增的，在(1,3)内是单调减的，在(3,+∞)内又是单调增的.而在邻域(1-δ,1+δ)，恒有f(x)≤f(1)；在邻域(3-δ,3+δ)，恒有f(x)≥f(3).所以f(1)=20为f(x)的极大值，点1为极大值点；而f(3)=16为f(x)的极小值，点3为极小值点.从f(x)=x³-6x²+9x+16的图象上，可以直观地看到它在(-∞,1)内上升，在(1,3)内下降，在(3,+∞)内上升，而点(1,20)是曲线上一个高峰，点(3,16)是曲线上一个低谷(如图1).实际上它们分别反映出函数的极大值和极小值.
函数的极值只是在一点的邻域这样一个很小范围内的最大值和最小值，所以它是局部性的.一个定义在区间〔a.b〕上的函数可以有许多个极大值和极小值，并且其中极大值不一定都大于每一个极小值(如图2).

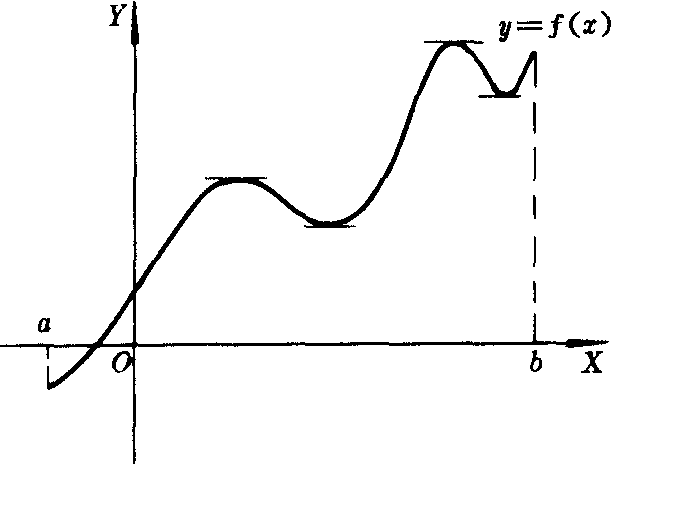
图2

确定一个函数的极值，可以有很多方法.最基本的方法是从判断函数的增减性中求得函数的极值.特殊地，对二次函数可以用配方法；对某些函数可以利用平均值不等式；对某些有理函数可以用判别式法.更一般的方法是利用微积分的有关知识求出函数的极值.