树干曲线stem curve

指沿树干中心假设的主干轴剖开形成树干的纵剖面，在剖面外缘所形成的曲线。用于描述树干形状。通常将树干的横断面近似地视为圆形，其半径为树干横截面长、短径的平均值。因此树干曲线一般是指树干平均半径与其所在树干上位置距树梢距离的函数图象。将树梢顶点置于直角坐标原点，树干中轴与x轴重合，则树干曲线方程为y=f(x)。树干曲线自基部向梢端的变化大致可归纳为凹曲线、平行于x轴的直线、抛物线和相交于x轴的直线等4种曲线类型。若将树干视为干曲线以x轴为轴的旋转体，则4种曲线的体型依次为截顶凹曲线体、圆柱体、截顶抛物线体和圆锥体。

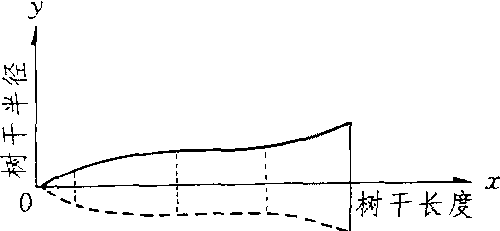
树干曲线示意图