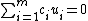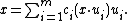“John ellipsoid”的意思、由来-开放百科全书

In mathematics, the John ellipsoid or Löwner-John ellipsoid E(K) associated to a convex body K in n-dimensional Euclidean space Rⁿ is the ellipsoid of maximal n-dimensional volume contained within K. The John ellipsoid is named after the German-American mathematician Fritz John.

In 1948, Fritz John proved^[1] that each convex body in Rⁿ contains a unique ellipsoid of maximal volume. Thus, each convex body has an affine image whose ellipsoid of maximal

volume is the Euclidean unit ball. He also gave necessary and sufficient conditions for this ellipsoid to be a ball.

The following refinement of John's original theorem, due to Keith Ball,^[2] gives necessary and sufficient conditions for the John ellipsoid of K to be a closed unit ball B in Rⁿ:

The John ellipsoid E(K) of a convex body K ⊂ Rⁿ is B if and only if B ⊆ K and there exists an integer m ≥ n and, for i = 1, ..., m, real numbers c_i > 0 and unit vectors u_i ∈ Sⁿ⁻¹ ∩ ∂K such that

A useful fact is that the dilation by factor

of a John ellipsoid contains the convex body^[1].

Applications

See also

References

1. ^¹John, Fritz. "Extremum problems with inequalities as subsidiary conditions". Studies and Essays Presented to R. Courant on his 60th Birthday, January 8, 1948, 187—204. Interscience Publishers, Inc., New York, N. Y., 1948. {{oclc|1871554}} {{MR|30135}}
2. ^{{cite journal| last = Ball| first = Keith M.| title = Ellipsoids of maximal volume in convex bodies| journal = Geom. Dedicata| volume = 41| year = 1992| issue = 2| pages = 241–250| issn = 0046-5755| doi = 10.1007/BF00182424|arxiv = math/9201217}}
3. ^{{cite journal|last1=Rimon|first1=Elon|last2=Boyd|first2=Stephen|title=Obstacle Collision Detection Using Best Ellipsoid Fit|journal=Journal of Intelligent and Robotic Systems|volume=18|issue=2|pages=105–126|doi=10.1023/A:1007960531949|year=1997}}
4. ^{{cite journal|last1=Shen|first1=Weiwei|last2=Wang|first2=Jun|title=Transaction costs-aware portfolio optimization via fast Löwner-John ellipsoid approximation|journal=Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence (AAAI2015)|year=2015|pages=1854–1860|url=https://pdfs.semanticscholar.org/7b31/2141616f092137c12397a47d11d94ddcea78.pdf}}