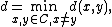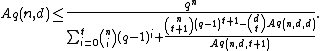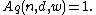- Definition
- See also
- References
In applied mathematics, the Johnson bound (named after Selmer Martin Johnson) is a limit on the size of error-correcting codes, as used in coding theory for data transmission or communications.
Definition
Let 
be a q-ary code of length 
, i.e. a subset of 
. Let 
be the minimum distance of , i.e.
where 
is the Hamming distance between 
and 
.
Let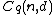 
be the set of all q-ary codes with length and minimum distance and let 
denote the set of codes in 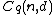such that every element has exactly 
nonzero entries.
Denote by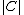 
the number of elements in . Then, we define 
to be the largest size of a code with length and minimum distance :
Similarly, we define 
to be the largest size of a code in :
Theorem 1 (Johnson bound for
):If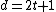 
,
If 
,
Theorem 2 (Johnson bound for
):(i) If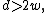 
(ii) If 
, then define the variable 
as follows. If is even, then define through the relation 
; if is odd, define through the relation 
. Let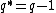 
. Then,
where 
is the floor function.
Remark: Plugging the bound of Theorem 2 into the bound of Theorem 1 produces a numerical upper bound on .
See also
- Singleton bound
- Hamming bound
- Plotkin bound
- Elias Bassalygo bound
- Gilbert–Varshamov bound
- Griesmer bound
References
- {{cite journal |first=Selmer Martin |last=Johnson |author-link=Selmer Martin Johnson |title=A new upper bound for error-correcting codes |journal=IRE Transactions on Information Theory |pages=203–207 |date=April 1962}}
- {{cite book |first1=William Cary |last1=Huffman |first2=Vera S. |last2=Pless |author-link2=Vera Pless |title=Fundamentals of Error-Correcting Codes |publisher=Cambridge University Press |year=2003 |isbn=978-0-521-78280-7}}
- FC Brugg
- FC Brunsviga 1896 Braunschweig
- FC Bruxelles
- FC Brăila
- FCBS
- FC Buelach
- FC Buffalo
- FC buffalo
- FC Buffalo Blitzers
- FC Buftea
- FC Bulach
- FC Bulat Cherepovets
- FC Bulle
- FC Bunyodkor
- FC Burevestnik-YuRGUES Shakhty
- F. C. Burkett
- FC Burlak Rybinsk
- FC Burnand
- FC Burovik Almetyevsk
- FC Buryatia Ulan-Ude
- FC Busingen
- FC Bârlad
- FC Bülach
- FC Büsingen
- F.C.C