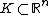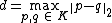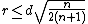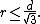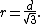“Jung's theorem”的意思、由来-开放百科全书

词条

Jung's theorem

释义

Statement
Jung's theorem in the plane
General metric spaces
References
External links

In geometry, Jung's theorem is an inequality between the diameter of a set of points in any Euclidean space and the radius of the minimum enclosing ball of that set. It is named after Heinrich Jung, who first studied this inequality in 1901.

Statement

Consider a compact set

and let

be the diameter of K, that is, the largest Euclidean distance between any two of its points. Jung's theorem states that there exists a closed ball with radius

that contains K. The boundary case of equality is attained by the regular n-simplex.

Jung's theorem in the plane

Most common is the case of Jung's theorem in the plane, that is n = 2. In this case the theorem states that there exists a circle enclosing all points whose radius satisfies

No tighter bound on r can be shown: when K is an equilateral triangle (or its three vertices), then

General metric spaces

For any bounded set S in any metric space, d/2 ≤ r ≤ d. The first inequality is implied by the triangle inequality for the center of the ball and the two diametral points, and the second inequality follows since a ball of radius d centered at any point of S will contain all of S. In a uniform metric space, that is, a space in which all distances are equal, r = d. At the other end of the spectrum, in an injective metric space such as the Manhattan distance in the plane, r = d/2: any two closed balls of radius d/2 centered at points of S have a nonempty intersection, therefore all such balls have a common intersection, and a radius d/2 ball centered at a point of this intersection contains all of S. Versions of Jung's theorem for various non-Euclidean geometries are also known (see e.g. Dekster 1995, 1997).

References

{{cite journal

| author = Katz, M.
| title = Jung's theorem in complex projective geometry
| journal = Quart. J. Math. Oxford
| volume = 36
| issue = 4
| year = 1985
| pages = 451–466
| doi = 10.1093/qmath/36.4.451}}

{{cite journal

| author = Dekster, B. V.
| title = The Jung theorem for the spherical and hyperbolic spaces
| journal = Acta Math. Hungar.
| volume = 67
| issue = 4
| year = 1995
| pages = 315–331
| doi = 10.1007/BF01874495}}

{{cite journal

| author = Dekster, B. V.
| title = The Jung theorem in metric spaces of curvature bounded above
| journal = Proceedings of the American Mathematical Society
| volume = 125
| issue = 8
| year = 1997
| pages = 2425–2433
| doi = 10.1090/S0002-9939-97-03842-2}}

{{cite journal

| author = Jung, Heinrich
| title = Über die kleinste Kugel, die eine räumliche Figur einschließt
| journal = J. Reine Angew. Math.
| volume = 123
| year = 1901
| pages = 241–257
| url = https://eudml.org/doc/149122
| language = German}}

{{cite journal

| author = Jung, Heinrich
| title = Über den kleinsten Kreis, der eine ebene Figur einschließt
| journal = J. Reine Angew. Math.
| volume = 137
| year = 1910
| pages = 310–313
| url = https://eudml.org/doc/149324
| language = German}}

{{cite book

|author1=Rademacher, Hans |author2=Toeplitz, Otto | title = The Enjoyment of Mathematics
| year = 1990
| publisher = Dover
| isbn = 978-0-486-26242-0
| nopp = true
| page = chapter 16}}

External links

{{mathworld | title = Jung's Theorem | urlname = JungsTheorem}}

4 : Geometric inequalities|Euclidean geometry|Theorems in geometry|Metric geometry

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。