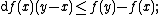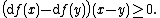“Kachurovskii's theorem”的意思、由来-开放百科全书

词条

Kachurovskii's theorem

释义

Statement of the theorem
References

In mathematics, Kachurovskii's theorem is a theorem relating the convexity of a function on a Banach space to the monotonicity of its Fréchet derivative.

Statement of the theorem

Let K be a convex subset of a Banach space V and let f : K → R ∪ {+∞} be an extended real-valued function that is Fréchet differentiable with derivative df(x) : V → R at each point x in K. (In fact, df(x) is an element of the continuous dual space V^∗.) Then the following are equivalent:

f is a convex function;
for all x and y in K,

df is an (increasing) monotone operator, i.e., for all x and y in K,

References

{{cite journal

| last = Kachurovskii
| first = I. R.
| title = On monotone operators and convex functionals
| journal = Uspekhi Mat. Nauk
| volume = 15
| number = 4
| year = 1960
| pages = 213–215
}}

{{cite book

}} {{MathSciNet|id=1422252}} (Proposition 7.4)

2 : Convex analysis|Theorems in functional analysis

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。