椭圆tuoyuan
平面内到两个定点F1,F2的距离的和等于定长(大于|F1F2|)的点的轨迹.这两个定点F1,F2叫做椭圆的焦点,两焦点间的距离叫做焦距,换言之,椭圆就是点集{M||MF1|+|MF2|=2a,2a>|F1F2|} (如图1).
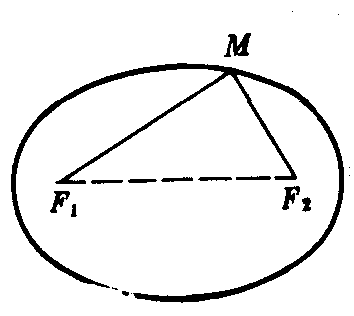
图1
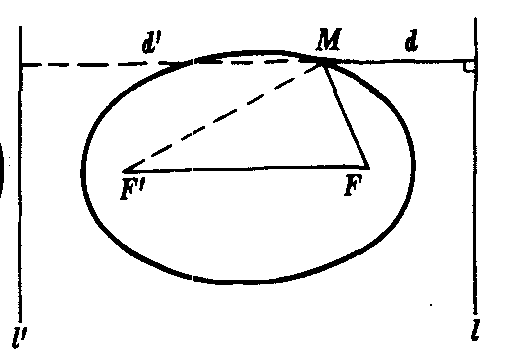
图2
当一个动点到一个定点F的距离和它到一条定直线l的距离之比是一个小于1的常数e时,这个动点轨迹是椭圆,这个定点F是椭圆的一个焦点,这条定直线l是椭圆的一条准线,这个常数e是椭圆的离心率.换言之,椭圆是点集{M||MF|/d=e,0
用不过圆锥顶点的平面截正圆锥面,当截面和圆锥的轴的交角θ满足α<θ<90°(a是圆锥的半顶高)时,截得的交线是椭圆(如图3).
用和圆柱的轴相交而不垂直于轴的平面截直圆柱面,截得的交线是椭圆(如图4).
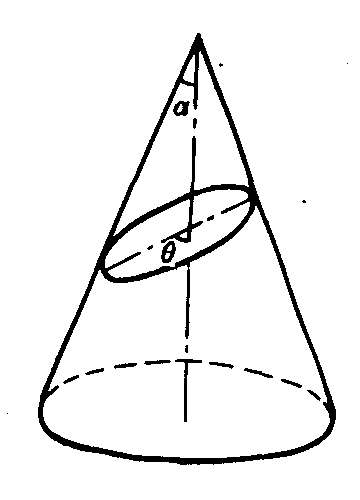
图3
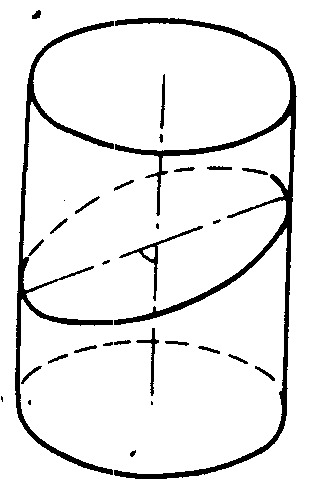
图4
椭圆tuoyuan
在平面内,到两定点的距离之和等于定长的点的集合,叫椭圆。两个定点叫椭圆的焦点,焦点之间的距离叫焦距。为了便于幼儿理解,可以将一条线绳两端固定在黑板上,线绳要拉开距离,比两固定点之间的距离长,能够垂下,如图(A);然后用一支笔按在线绳任意位置上,将线绳拉直(B);这时移动笔,要一直使线绳保持绷直状态,于是画出一个椭圆来(C)。