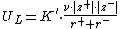- Derivation from the Born–Landé equation
- See also
- References
- Literature
The Kapustinskii equation calculates the lattice energy UL for an ionic crystal, which is experimentally difficult to determine. It is named after Anatoli Fedorovich Kapustinskii who published the formula in 1956.[1]
| where | K = 1.20200{{e>−4}} J·m·mol−1 |
| d = 3.45{{e>−11}} m | |
| ν is the number of ions in the empirical formula, | |
| z+ and z− are the numbers of elementary charge on the cation and anion, respectively, and | |
| r+ and r− are the radii of the cation and anion, respectively, in meters. |
The calculated lattice energy gives a good estimation; the real value differs in most cases by less than 5%.
Furthermore, one is able to determine the ionic radii (or more properly, the thermochemical radius) using the Kapustinskii equation when the lattice energy is known. This is useful for rather complex ions like sulfate (SO{{su|b=4|p=2−}}) or phosphate (PO{{su|b=4|p=3−}}).
Derivation from the Born–Landé equation
{{Further information|Born–Landé equation}}Kapustinskii originally proposed the following simpler form, which he faulted as "associated with antiquated concepts of the character of repulsion forces".[1][2]
Here, K
Kapustinskii replaced r0, the measured distance between ions, with the sum of the corresponding ionic radii. In addition, the Born exponent, n, was assumed to have a mean value of 9. Finally, Kapustinskii noted that the Madelung constant, M, was approximately 0.88 times the number of ions in the empirical formula.[2] The derivation of the later form of the Kapustinskii equation followed similar logic, starting from the quantum chemical treatment in which the final term is {{nowrap|1 − {{sfrac|d|r0}}}} where d is as defined above. Replacing r0 as before yields the full Kapustinskii equation.[1]
See also
- Born-Haber cycle
References
2. ^1 2 {{Cite book|url=https://books.google.ie/books?id=dzjxzsKjZGUC|title=Metals and Chemical Change|last=Johnson|first=David Arthur|publisher=Royal Society of Chemistry|year=2002|isbn=0854046658|volume=1|location=|pages=135-136}}
Literature
- A. F. Kapustinskii; Z. Phys. Chem. Abt. B Nr. 22, 1933, pp. 257 ff.
- A. F. Kapustinskii; Zhur. Fiz. Khim. Nr. 5, 1943, pp. 59 ff.
- Coobowie, South Australia
- Cooccurrence
- Co-occurring disorders
- Cooch Behar I
- Cooch Behar I (Community development block)
- Cooch Behar II
- Cooch Behar II (Community development block)
- Coochbehar (Lok Sabha constituency)
- Cooch Behar Panchanan Barma University
- Cooch Behar railway station
- Cooch Behar Rambhola High School
- Cooch Behar State Railway
- Cooch Behar University
- Cooch (disambiguation)
- Coochi
- COO (chief operating officer)
- Coochie Harris
- Coochiemudlo Island, Queensland
- Coochin Coochin Homestead
- Coochin Creek
- Coochin Creek, Queensland
- Coockies
- Coode
- Coode Canal
- Coode, John