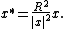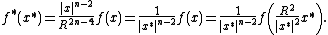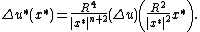“Kelvin transform”的意思、由来-开放百科全书

词条

Kelvin transform

释义

See also
References

This article is about a type of transform used in classical potential theory, a topic in mathematics.

The Kelvin transform is a device used in classical potential theory to extend the concept of a harmonic function, by allowing the definition of a function which is 'harmonic at infinity'. This technique is also used in the study of subharmonic and superharmonic functions.

In order to define the Kelvin transform f^* of a function f, it is necessary to first consider the concept of inversion in a sphere in Rⁿ as follows.

It is possible to use inversion in any sphere, but the ideas are clearest when considering a sphere with centre at the origin.

Given a fixed sphere S(0,R) with centre 0 and radius R, the inversion of a point x in Rⁿ is defined to be

A useful effect of this inversion is that the origin 0 is the image of , and is the image of 0. Under this inversion, spheres are transformed into spheres, and the exterior of a sphere is transformed to the interior, and vice versa.

The Kelvin transform of a function is then defined by:

If D is an open subset of Rⁿ which does not contain 0, then for any function f defined on D, the Kelvin transform f^* of f with respect to the sphere S(0,R) is

One of the important properties of the Kelvin transform, and the main reason behind its creation, is the following result:

Let D be an open subset in Rⁿ which does not contain the origin 0. Then a function u is harmonic, subharmonic or superharmonic in D if and only if the Kelvin transform u^* with respect to the sphere S(0,R) is harmonic, subharmonic or superharmonic in D^*.

This follows from the formula

References

William Thomson, Lord Kelvin (1845) "Extrait d'une lettre de M. William Thomson à M. Liouville", Journal de Mathématiques Pures et Appliquées 10: 364–7
William Thompson (1847) "Extraits deux lettres adressees à M. Liouville, par M. William Thomson", Journal de Mathématiques Pures et Appliquées 12: 556–64
{{cite book | author = J. L. Doob | title = Classical Potential Theory and Its Probabilistic Counterpart |page=26| publisher = Springer-Verlag | year = 2001 | isbn=3-540-41206-9 }}
{{cite book | author = L. L. Helms | title = Introduction to potential theory | publisher = R. E. Krieger | year = 1975 | isbn=0-88275-224-3 }}
{{cite book | author = O. D. Kellogg | title = Foundations of potential theory | publisher = Dover | year = 1953 | isbn=0-486-60144-7 }}
John Wermer (1981) Potential Theory 2nd edition, page 84, Lecture Notes in Mathematics #408 {{ISBN|3-540-10276-0}}

3 : Harmonic functions|Transforms|William Thomson, 1st Baron Kelvin

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

See also

References