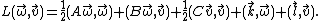“Kirchhoff equations”的意思、由来-开放百科全书

词条

Kirchhoff equations

释义

References

In fluid dynamics, the Kirchhoff equations, named after Gustav Kirchhoff, describe the motion of a rigid body in an ideal fluid.

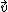where and are the angular and linear velocity vectors at the point , respectively; is the moment of inertia tensor, is the body's mass; is

a unit normal to the surface of the body at the point ;

is a pressure at this point; and are the hydrodynamic

torque and force acting on the body, respectively;

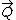and likewise denote all other torques and forces acting on the

body. The integration is performed over the fluid-exposed portion of the

body's surface.

If the body is completely submerged body in an infinitely large volume of irrotational, incompressible, inviscid fluid, that is at rest at infinity, then the vectors and can be found via explicit integration, and the dynamics of the body is described by the Kirchhoff – Clebsch equations:

Their first integrals read

.

Further integration produces explicit expressions for position and velocities.

References

Kirchhoff G. R. Vorlesungen ueber Mathematische Physik, Mechanik. Lecture 19. Leipzig: Teubner. 1877.
Lamb, H., Hydrodynamics. Sixth Edition Cambridge (UK): Cambridge University Press. 1932.

4 : Mechanics|Classical mechanics|Rigid bodies|Gustav Kirchhoff

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。