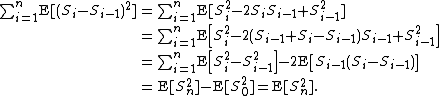“Kolmogorov's inequality”的意思、由来-开放百科全书

词条

Kolmogorov's inequality

释义

Statement of the inequality
Proof
See also
References

In probability theory, Kolmogorov's inequality is a so-called "maximal inequality" that gives a bound on the probability that the partial sums of a finite collection of independent random variables exceed some specified bound. The inequality is named after the Russian mathematician Andrey Kolmogorov.{{Citation needed|date=May 2007}}

Statement of the inequality

Let X₁, ..., X_n : Ω → R be independent random variables defined on a common probability space (Ω, F, Pr), with expected value E[X_k] = 0 and variance Var[X_k] < +∞ for k = 1, ..., n. Then, for each λ > 0,

where S_k = X₁ + ... + X_k.

The convenience of this result is that we can bound the worst case deviation of a random walk at any point of time using its value at the end of time interval.

Proof

{{Multiple issues|section=yes|{{Unreferenced section|date=November 2017}}{{Disputed-section|date=November 2017}}
}}

The following argument is due to Kareem Amin and employs discrete martingales.

As argued in the discussion of Doob's martingale inequality, the sequence is a martingale.

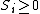Without loss of generality, we can assume that and for all .

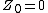Define as follows. Let , and

for all .

Then is also a martingale. Since 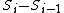is independent and mean zero,

The same is true for . Thus

by Chebyshev's inequality.

This inequality was generalized by Hájek and Rényi in 1955.

References

{{cite book | last=Billingsley | first=Patrick | title=Probability and Measure | publisher=John Wiley & Sons, Inc. | location=New York | year=1995 | isbn=0-471-00710-2}} (Theorem 22.4)
{{cite book | last=Feller | first=William | authorlink=William Feller | title=An Introduction to Probability Theory and its Applications, Vol 1 | edition=Third | origyear=1950 | year=1968 | publisher=John Wiley & Sons, Inc. | location=New York | isbn=0-471-25708-7 | nopp=true | page=xviii+509 }}

3 : Stochastic processes|Probabilistic inequalities|Articles containing proofs

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Statement of the inequality

Proof

See also

References