气压qiyaatmospheric pressure
气象要素之一, 是与大气接触的表面上, 由于空气分子的碰撞在单位面积上所受到的力。又名大气压强或大气压力。其大小不因接触面的方向而异。这个力与大气重量有关, 即承受其上大气层施加的力。故气压的数值等于该高度上单位横截面的垂直空气柱的重量。单位 用来表示气压的国际单位为帕斯卡, 简称帕(Pa), 1帕定义为1牛顿/米2。在流体力学中常用巴(bar), 1巴等于106达因/厘米2。气象学中常取毫巴(mb)为单位, 即1毫巴=103达因/厘米2。1mb=1hPa(百帕), 所以500mb也称500 hPa。还常用水银柱高度(mmHg, 或简称mm)来表示气压的大小。1mm或称1托 (Torr)=133.3224Pa=1.333224hPa=4/3mb。这里的水银柱高度指标准密度的水银(13.5951克/厘米3)处于标准重力(980.665厘米/秒2)条件下用以平衡大气压强的水银柱高度。国际上规定在标准重力、气温为0℃条件下, 单位(平方厘米)面积上承受760mmHg=1013.25mb=101325Pa的压力称为标准大气压。
时空分布 气压按指数规律随高度递减。每上升约5.5公里, 气压递降一半。压高公式常表示为
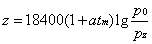
气压Qiya
大气垂直施加在一个单位平面面积上的作用力。在大气中任一固定地方,不论承受大气压力的表面是横放、竖放或侧放,其受到的大气压力大小都是一样的。在静稳大气中,任一高度上的气压值就等于该高度上单位面积所承受的大气柱重量。气压的单位为帕斯卡(pa)或毫巴(mb)。1毫巴=100帕斯卡,即在1个平方米面积上受到100牛顿的压力。气压单位也曾用气压表上的水银柱高度表示,称毫米水银柱高(mmHg ),简称毫米(mm)。1毫米水银柱高=1.33 322毫巴≈4/3毫巴。国际规定在温度为0℃,纬度为45°的海平面上,760毫米水银柱高为一个大气压。因此:一个大气压=760毫米水银柱高=760×1.33 322毫巴=1 013.25毫巴=1 013.25百帕。气压在垂直和水平方向上都有变化。大气层如同海洋一样,在底层压力最大,随着高度的增加压力逐渐减小,海平面上的气压一般在1 000百帕左右,而到达5 500米上空,气压只有500百帕,比海平面减小了一半。到12 000米高空,气压减为200百帕左右,到16 000米处,气压只有100百帕左右了。虽然气压随高度增加而减小,但减小的快慢程度却随空气密度的不同而有差异。密度大的地方,气压随高度递减得快些;密度小的地方,气压随高度递减得慢些。由于热力和动力的原因,在同一水平面上气压的分布也是不均匀的。在一般情况下,气温升高,近地面大气受热膨胀上升,到高空堆积,密度增大,那里的气压比同一水平面上周围的气压高,形成高压区。因而空气便从高压区向周围气压低的地区扩散,使这一地区整个大气柱的空气减少,地面上承受的大气压力降低,形成低气压。同理,气温降低,气压升高。气压的高低是空气水平运动的推动力,气流总是由气压较高的地方向气压较低的地方流动。一般说来,海拔高度在1 000米以下的中纬度地区,大陆上的气压在冬季比春、夏、秋三季略高,在夏季比冬、春、秋三季略低。然而,在大陆的更高高度以及在海面上情况正好相反。在春、秋季,在中纬度陆地常经历到高、低压系统交替出现,气压的变化是,在低压中心通过时它比正常值低15—25毫巴,而在高压中心通过时它比正常值高约15—20毫巴。在夏季中纬度的气压变化周期一般较长,而振幅比寒冷的季节为小。在热带地区,一季中只有少数几个主要的高、低压系统通过,气压的日变化一般有两个最大值,约在上午10点与下午10点;两个最小值,约在上午4点与下午4点。气压日较差随纬度增高而减小。气压的实际重要性在于它与风和天气的关系。气压差异引起风的形成(参阅“风”条)。高压区的空气下沉,由于绝热压缩而增温和变干燥,使天气晴朗;低压区的空气上升,冷却和凝结,产生云和雨的天气。
气压Qiya
大气垂直施加在一个单位平面面积上的作用力。实际是压强,习惯称气压。单位是帕斯卡(pa)。一个地方的气压等于由该处垂直向上一直延伸到大气上界的大气柱的重量。不同高度,承受的大气柱重量不同气压也不同,位置愈高、大气柱愈短、大气柱重量愈小,气压就愈小。反之,位置愈低,气压愈高。海平面气压最高。一般以海平面上大气压力的平均值作为一个大气压,其值大约等于1 000百帕,近似1公斤重/厘米2。但是大气中空气分子在底层密集,在高层稀疏,以致大气压力随高度的减小在底层比高层迅速。例如,从海平面到5 500米高空,气压减少到海平面的一半,而从5 500米到10 000米高空,气压却只减少了海平面气压的1/4。
地球上气压分布是连续的。由于地表热力分布不均和地转偏向力影响,表现出纬向带状分布规律。极地是地球的冷极,空气冷缩聚积在低空,形成高压。赤道是地球的热区,空气膨胀上升、外流,低空形成低压,称赤道低压。在不旋转的地球上,应该出现低空从极地高压流向赤道低压的气流,高空出现从赤道高空流向极地高空的气流,两者组成一个完整的南北向的环流圈。然而地球是自转的,自转的结果产生了地球偏转力,偏转力使南北向(经向)的环流圈难以实现,并发生方向偏转。比如从赤道高空流向极地的气流在地转偏向力作用下不断向右偏(北半球),当气流到达30°N附近时,风向已经偏转成西风了,结果阻碍了赤道来的气流北进,而大量在30°N附近聚积形成高压带,称副热带高压带。在副热带高压带和极地高压带之间是一个相对的低压带,称副地低压带。这样在北半球(或南半球)形成四个纬向的气压带,全球形成七个气压带。这些气压带的排列是高低相间的,对于全球风带的形成是重要的基础。纬向气压带由于下垫面海陆热力性质的明显差异,而发生破裂,分裂成几个孤立的高、低压单体。比如副热带高压分裂成夏威夷高压(在太平洋),和亚速尔高压(在大西洋);副极地低压分裂成阿留申低压(北太平洋)和冰岛低压(北大西洋)。这些高、低压终年存在,只是随季节而有范围、强度、位置的变化。面积广大的陆地,冬、夏季时,因热力作用,在低空可能出现与纬向气压带性质相反的气压单体,比如夏季亚洲南部的热低压,称南亚低压。冬季亚洲北部形成的冷高压,称蒙古高压。同样在北美大陆的西南部和北部各生成一个低压(夏季)、一个高压(冬季)。这些高、低压都控制着当地的气流运动,被称为大气活动中心。海洋上的气压中心终年存在,称为永久性活动中心, 陆地上只存在于半年, 称为季节性活动中心。
空中大气受种种因素影响,气压的分布十分复杂,形式多样,但基本形式是低压、低压槽、高压、高压脊和鞍形区(两高压两低压交互排列,如同马鞍)。这些不同的气压型产生着不同的天气。
气压atmospheric pressure
又称大气压力、大气压强。单位面积上承受的大气重力,其数值等于从单位底面积向上,一直延伸到大气上界的垂直气柱的重力。气象上规定1个标准大气压是1013.25百帕(hPa)或毫巴(mbar),相当于760 mm的水银柱。国际上是将纬度45°的海平面上,温度0℃时、760mmHg高的气压,作为1个标准大气压。气压按指数规律随高度递减,在5.5 km高度上,气压约为海平面气压的一半。气压在水平方向的分布并不均一,其差异引起空气的水平流动。
气压
自然环境要素。天水市年平均气压833.9~894.1百帕 (测站记录),年平均最高气压835.8~896.6百帕,年平均最低气压831.5~890.9百帕。气压随海拔高度增高而下降。月平均气压最低出现在7月,为811.4百帕,最高出现在11月,为900.4百帕。
气压
各地气压年平均值在970~1010毫巴之间。年变化以1月最高,7月最低。气压年较差各地多在20毫巴左右,但其变化程度受海拔影响较大,气压年较差随高度增加而显著减小(如衡阳年较差21.8毫巴,南岳高山只有10.3毫巴)。在通常情况下,气压日变化呈两高两低型周期变化,最高出现在午前10时前后,次高在22时左右,最低出现在午后3时到5时,次低在早晨4时至5时。此外,气压还有着非周期的变化,其变化数值较大,且时间不定,持续时间长短不一,如在热带气旋侵袭时,和在龙卷风区域里,以及在强烈的雷雨发生时,能引起气压短时的突然升降。
气压
大气受地心引力而产生的压力。大气作用在单位面积上的力叫大气压强,又称大气压。在纬度45°,气温0℃,海拔高度0 m的大气压为1013.25 hPa,相当于760 mm高水银柱的压强。实际大气的气压变化很大,高气压中心达1070 hPa,低气压中心达970 hPa,龙卷风低达200~400 hPa。各地气压差的存在造成空气流动。高气压空气下沉,多好天;低气压空气上升,易云雨。