- Introduction
- Presentation
- Matrix Representation
- Generalizations
- See also
- References
In mathematics, the lamplighter group L of group theory is the restricted wreath product 
Introduction
The name of the group comes from viewing the group as acting on a doubly infinite sequence of street lamps 
each of which may be on or off, and a lamplighter standing at some lamp 
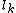. An equivalent description for this, called the base group 
of 
is
,
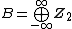an infinite direct sum of copies of the cyclic group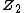 
where 
corresponds to a light that is off and 
corresponds to a light that is on, and the direct sum is used to ensure that only finitely many lights are on at once. An element of 
gives the position of the lamplighter, and to encode which bulbs are illuminated.
There are two generators for the group: the generator t increments k, so that the lamplighter moves to the next lamp (t -1 decrements k), while the generator a means that the state of lamp lk is changed (from off to on or from on to off.) Group multiplication is done by "following" these operations.
Presentation
The standard presentation for the lamplighter group arises from the wreath product structure
, which may be simplified to
.
The generators a and t are intrinsic to the group's notable growth rate, though they are sometimes replaced with a and at, changing the logarithm of the growth rate by at most a factor of 2.
We may assume that only finitely many lamps are lit at any time, since the action of any element of L changes at most finitely many lamps. The number of lamps lit is, however, unbounded. The group action is thus similar to the action of a Turing machine.
Matrix Representation
Allowing 
to be a formal variable, the lamplighter group is isomorphic to the group of matrices
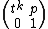
where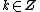 
and 
ranges over all polynomials in 
.[1]
Using the presentations above, the isomorphism is given by
.
Generalizations
One can also define lamplighter groups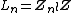 
, with 
, so that "lamps" may have more than just the option of "off" and "on." The classical lamplighter group is recovered when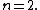 
See also
- Growth rate (group theory)
References
- Volodymyr Nekrashevych, 2005, Self-Similar Groups, Mathematical Surveys and Monographs v. 117, American Mathematical Society, {{isbn|0-8218-3831-8}}.
- Artem Blazhiyevsky
- Artem Bloshenko
- Artem Bludnov
- Artem Borodkin
- Artem Bykov
- Artem Chebotarev
- Artem Chernov
- Artem Chesakov
- Artem Chorniy
- Artem Concharenko
- Artem Demkov
- Artem Derepasko
- Artem (disambiguation)
- Artem Dorofeyev
- Artem Dubinin
- Artem Dudolev
- Artem Dyatlov
- Artemenko
- Artemesia Formation
- Artem Falyan
- Artem Favorov
- Artem Fedchuk
- Artem Fedetskiy
- Artem Fedyanin
- Artem Filimonov